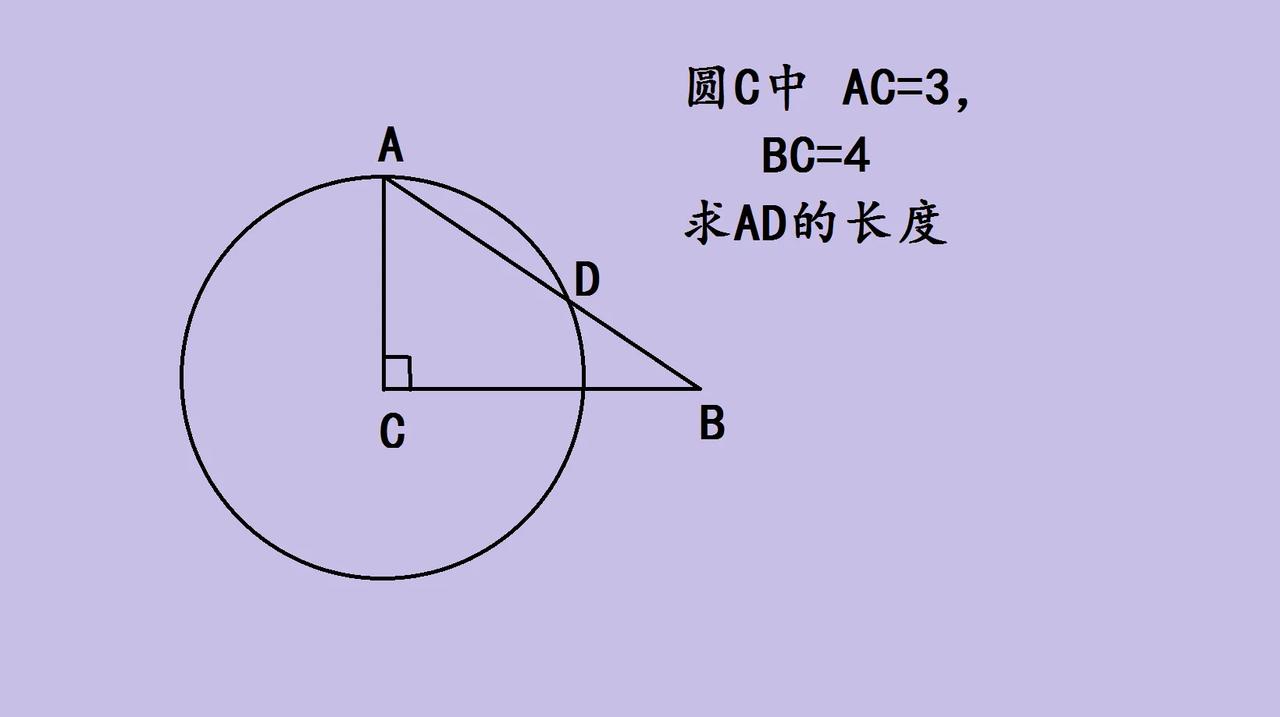
初中几何，圆C中，AC=3，BC=4，求AD长度。首先，AC是圆的半径，因为AC垂直于BC，这直角很关键。 从图里能看到，AC、BC构成直角三角形的两条直角边，或许能利用勾股定理先找AB长度，再结合圆的性质，比如切割线定理？因为AB是从圆外一点B到圆的一条割线，BD和BA可能满足切割线关系（虽然这里不是切线，但割线定理适用）。 不过具体咋算咱先不说过程，就说几何题的有趣之处，把圆、直角三角形这些知识串一块，像拼拼图，找到各边关系，就能推出AD长度。 数学里的几何题，就像藏着小宝藏，一步步挖掘条件，把零散知识连成线，就能解开谜底。这道题看着简单，却融合圆的半径、直角三角形、割线定理（或相似三角形），是锻炼思维的好题，你要不要试试找AD的长度呀，解出来超有成就感～
评论列表
猜你喜欢
【2评论】【10点赞】
【1评论】【5点赞】
【1评论】【1点赞】
【99评论】【99点赞】
【6点赞】
【2评论】【2点赞】
【4评论】【1点赞】
【3评论】【3点赞】
作者最新文章
热门分类
用户16xxx08
延长AC至圆边E、连接DE、可得AED相似ABC 由图中条件可知三角形ACD为直角三角形、勾股定理可得AB=5 利用相似从而可解AD=3.6