编辑：编辑部

一道看似简单的概率谜题，竟然让80%的人都做错了？

这道题如下——

你有一个装有100个球的罐子，罐子看不到里面，其中有n个红球，「100-n」个绿球。n为「0,100」之间的一个随机数。

你伸手进入罐子并取出一个球，它是红色的，把它扔掉后，如果你现在再取出一个球，它更有可能是红色还是绿色？或者两种颜色的可能性是相等的？

目前，已经有两万多人对这道题进行了投票，但是，只有22%的人做对了。

你的答案是什么？请等待后文公布正确答案。

今年1月份，当数学家Daniel Litt在网上发出这道题后，引爆了众多数学家、计算机科学家和经济学家的解题热情！

有研究者声称，自己如此沉迷于这道题，以至于正经研究都无心去做了

甚至，还有一些哲学家、金融家、体育分析师参与了进来。

甚至，这道谜题还催生了一系列相关论文，来探讨谜题背后的数学意义！

论文地址：https://sites.math.rutgers.edu/~zeilberg/mamarim/mamarimhtml/MihaiNicaAliceBob.pdf

论文地址：https://arxiv.org/pdf/2405.16660

论文地址：https://arxiv.org/pdf/2406.20049

可以说，这道在线谜题真正凸显了脑筋急转弯对于大众的持久吸引力。

而且，它还展示出了我们数学直觉的局限性，以及概率推理的反直觉性。

Litt表示，没有什么比出一道多项选择题更令人兴奋的了，而且50000人的成绩甚至比随机选择的还要差

这道题，究竟为什么如此反直觉？为什么简单的概率问题，会如此出人意料地困难？

让我们仔细讨论一下，是什么造就了一个伟大的谜题。

选中红球，下一个球是什么？

话说回来，在这道罐子谜题中，你的答案是什么？

下面公布正确答案——红色。

怎么样，的确十分反直觉吧。

为什么答案不是绿色，或二者概率相等呢？

Litt表示，这位来自伦敦的数学研究者George Lowther的解释，给出了自己最为喜欢的思考方式——

想象一下，一开始有101个球排成一行，而非100个球，再随机挑选一个球。

然后，把它左边的球涂成绿色，右边的球涂成红色，再把手里的球扔掉，便剩下100个球。

然后，随机选择第二个球，这个球对应原问题中的第一个球。问题告诉你，你选了一个红球，所以它在你扔掉的球的右边。

现在挑选第三个球，这个球有三种可能的位置：

1）在第一个球的左边

2）在第一个球和第二个球之间

3）在第二个球的右边

在这三种可能性中，有两种情况下，第三个选中的球是红色的。所以球是红色的概率是2/3。

另一位统计学博士Jonatan Pallesen提出了一个很好的启发性解释：

如果你去钓鱼，并很快钓到一条鱼，便会期望湖里有更多的鱼。同样，如果你已经拿到一个红球，这表明罐子里有很多红球。

「反直觉陷阱」，为何如此有迷惑性

不过，这一问题恰恰反映出了一个反直觉的陷阱。

按理说，如果拿出了一个红球，那么瓮中红球的数量就减少了，所以下一个球就更有可能是绿色的。

很多人都是这么想的，然而，这是一个错误的直觉！

许多人坚持认为，因为红球数量减少，所以下一个球更有可能是绿色的。

Litt对此表示，「他们不愿意接受数学论证，但对模拟结果更具信服力」。

其实，这是一个随机选择的概率，但从中获得的信息，会影响我们对后续事件概率的判断。

一些参与者惊讶道，如此显而易见的答案，竟有很多人没有发现。

我确实感到惊讶的是，我们在这类问题上表现得如此糟糕，因为概率与现实世界的活动有着如此明显的相关性。我们必须不断地观察世界并评估可能性，然后决定行动方案。

或许这个问题确实对于一些专业人士来说，的确轻而易举。但多数人还是会掉入陷阱，为什么对他们来说，这道题会如此困难？

Litt认为，关键点在于初始设置中的概率分布。

也就是说，罐子问题是完全依赖于，红球数量是根据所谓的均匀分布（即从瓮中抽取）来选择的。

当抽出的是一个红球，告诉你的信息是，自己处于一个「红色的世界」中，但也只是因为Litt这样设置的问题。

但若是，根据二项分布来选择球的颜色——即通过抛硬币来选择每个球的颜色。

那么，即便你知道了第一个球是红色的，但对下一个球来说，没有什么含义，进而不会影响后续抽取概率。

修改起始分布非常容易，这样就能获得红色、绿色、或可能性等同的三种答案中的一种。

如果调整分布，就会完全改变答案，因此，一个人的直觉必须对问题的设置非常敏感，这才是解决此类问题的关键。

对此，Litt设计了一系列罐子问题，每一个都是为了打败某人为之前某个变体提出的启发性解释而设计的。

所以说，很难想出能够检测到这些细节的启发性方法。

其实，在现实世界中，我们在概率计算上，并非那么擅长。

但在生活中，有些活动却与概率问题息息相关。我们通过不断观察世界，评估概率，然后再做出行动方案。

Litt称，虽然我不是心理学专家，但人们在考虑问题各个方面，都会变现出规避风险，由此会系统地高估了/低估了极不可能发生事件的概率。

在线谜题，万人参战

一直以来，Litt专注于研究代数几何和数论交集的领域，而在概率论方面，他还只是业余爱好者。

过去，他参加了一些有关概率的讲座，并激发出极大的兴趣，跃跃欲试。

Litt表示，「虽然概率论与日常的数学思考内容，相去甚远，但也涉及到了自己一些相对熟悉的东西」。

闲暇时候，他会提出一些简单的概率问题。

当自己发现得到了一个很酷、且反直觉的答案时，便会将谜题发在X上，让大家一起破解。

人们喜欢在社交媒体上吐槽，Litt的谜题下面，也逐渐成为大家讨论的社区，构建起一个概率圈的生态系统。

之所以在X上讨论数学，是因为2020年疫情期间，Litt感到非常孤独，便发现在社交媒体中，与随机的人聊自己喜欢的主题可以获得快乐。

在Litt看来，即便是抛硬币这种最基本的概率事件，也会产生有趣的问题。

就比如，前段时间，他发布的有关掷硬币的一个谜题，便吸引了2万多人参与讨论。

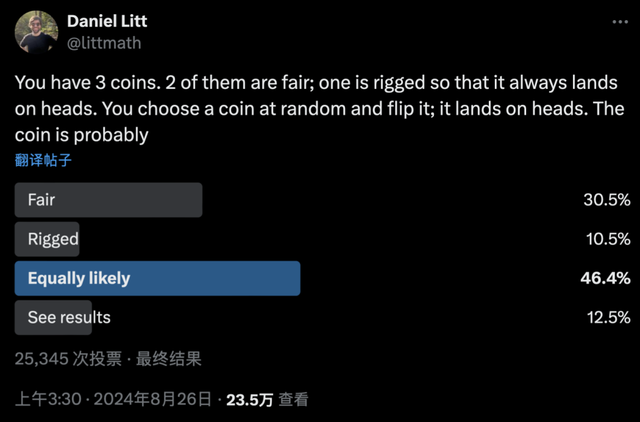
还有另一个改版的同类谜题，更是得到近5万位网友的投票。

下一个谜题：抛硬币

下面这道抛硬币难题，被Litt称为自己最喜欢的谜题。

而且，仅有10%的参与者答对了，比例低到惊人！

Alice和Bob各抛硬币100次（正面是H，反面是T）。每当连续出现两个正面HH时，Alice得1分；出现正反面HT时，Bob得1分。

因此，现在，二人已经得到了「THHHT」，因此Alice得2分，Bob得1分，最后谁更有可能获胜？

有人对此推理的是，如果列出100次抛硬币的所有不同结果，并计算出Alice和Bob的分数。他认为每个人总分相同。

因此，他们预期的答案是二者相同。

但事实证明，Bob获胜的可能性更大！这是为什么？

显然，人们的直觉又在作祟了。

一个直觉是，Alice可以在短时间内得很多分。例如，在连续出现正面HHHHHHH情况下，她在第一次之后的每次抛掷中都得分。

在100次抛掷中，Alice的分数可以高达99，但Bob最多只能得50分。

所以Alice会以压倒性的优势获胜，这意味着她在游戏中浪费了一些期望得分。

相较之下，Bob可能会赢得更多比赛，但每次获胜优势较小。通过模拟验证，可以证明这个结果是正确的。

不确定的是，如果改变游戏规则的话，这个启发性的方法是否成立。

而且，Litt表示，我不知道是否存在一个证明，能够完全解释这种现象，特别是一个适用于任意次数翻转的证明。

概率论家、数学博士发论文

对于自己所出的概率题，Litt也做了一个证明，但仅是一个复杂，且缺乏理论的论证。

而真正让他兴奋的是，这些谜题在一大波专业人士中，掀起了热议。

一位数学博士Sridhar Ramesh收集了一些漂亮的论证。

他将抛硬币问题比作成一个「随机行走」的问题，其中向上和向下的步骤概率相等，但速度分布不同。

从中可以获得的关键观察是，返回原点所需的时间，与第一步向上还是向下无关。

因为反向执行相同的步骤，也有相同的概率。

由此，可以得出，对于任何固定的行走时间，最后一步离开原点的方向（向上或向下）的概率是相等的。

那么，再将这个观察应用到硬币游戏中：

- HH相当于一个单位时间的「向上」步骤

- HT^n H相当于n+1个单位时间的向下步骤

这意味着，游戏结束时，我们同样可能在原点之上（Alice赢，或者存在一个可能让游戏平局HT^n H的中间步骤），或原点之下（Bob赢）。

如果游戏由HHT，后面全是T组成，有可能会平局。

由于可能在HT^n H步骤的中间结束，（在给Bob一个使游戏平局的分数后，但在返回到H之前），而不可能在HH的中间结束，所以Alice获胜的可能性比Bob小。

Litt还表示，有一大类问题是从最初抛硬币问题中衍生出来的。

对于这些问题，很多人提出了不错的论证，但他个人仍然觉得，无法实现直观的理解。至少从业余观点来看，其中有很多令人惊讶的有趣的数学。

另有一位来自罗格斯大学教授Doron Zeilberger，在这些问题中发现了有价值的内容，并发表了论文。

论文地址：https://arxiv.org/pdf/2405.13561

论文中， Zeilberger编写了一个软件包，用于分析这类概率问题的长期行为。

比如，他的程序可以证明在n次抛掷后（当n非常大时），平局的概率大约是1/√n乘以某个明确的常数。

他还计算了一些称为「矩」的量。

当你查看Alice和Bob的得分之间的所有可能差异，这些差异的平均值为0，这也是使其成为一个难题的部分原因。

但你也可以计算「二阶矩」，即对差异的平方求平均值，以及「三阶矩」，即对差异的立方求平均值等等。

Zeilberger和数学家Mihai Nica提出了一个猜想，即仅仅知道二阶和三阶矩，就足以确定谁赢得更多的比赛。

不过，Litt认为，这一点尚未完全证明。

而现在，又有后继者，另一位数学家Svante Janson以及Nica正在撰写一个证明。

答案&一道新题

以下三道题，答案会在后面公布。

第一题：Equally likely

第二题：HTTTH

第三题：Bob

就在刚刚，Litt又发布了一个改版的罐子问题，你认为答案会是哪个？

个人介绍

Daniel Litt目前是多伦多大学数学助理教授。2019-2022年，他也曾在佐治亚大学担任助理教授。

2015年，他获得了斯坦福大学博士学位。2018年在哥伦比亚大学担任NSF博士后。另外，2018-2019年，他还是高级研究所的成员。

总的来说，Litt对代数几何和数论之间的相互作用感兴趣，对拓扑学也有一定的兴趣。

他的大部分工作都集中在，使用算术技巧来研究比如复杂代数簇的经典问题。

目前，他的研究重点是，代数簇基本群上的算术结构，以及这些结构和簇的几何之间的关系。

此外，他本人其他感兴趣方向包括，关于正性和消失性定理的问题，代数簇的动力学，以及霍奇理论（广义理解）。

目前，他得到了NSERC的资助项目——算术和代数几何中的Anabelian方法，还曾是斯隆的研究奖学金获得者，以及安大略省的早期研究人员。