公元4世纪,亚历山大的希腊数学家Pappus发现,蜜蜂的蜂巢的六角形结构似乎是将二维空间划分为面积相等、周长最小的单元格(cells)的最佳方式(平铺二维空间),这使得蜜蜂减少了它们需要生产的蜂蜡的数量。

就单个圆而言,同样的面积,周长最小,但是当排列在一起时,就会有空隙,这样就不如六边形来得更经济。

但是几千年来,没有人能证明六边形是最优的,直到1999年,数学家托马斯·黑尔斯(Thomas Hales)最终证明,没有其他形状能比六边形更好。至于3维和更高维度的空间,数学家们仍然不知道哪些形状的单元格是最“经济”的平铺方式。
这个问题(称为泡沫问题)已经被证明具有广泛的应用,物理学家可以研究这些“泡沫(单元格)”的性质,化学家可以分析晶体的结构,数学家可以探索球体的排列方式,统计学家可以开发有效的数据处理技术。

最为重要的是,泡沫问题还与计算机科学有着深刻的联系,利用这种联系,计算机科学家能够找到一种新的具有最小表面积的高维形状。但这个形状缺少了一个重要的东西,几何基础。因为它的存在是用计算机科学技术证明的,所以它的实际几何形状很难掌握。这就是纽约大学的计算机科学家Oded Regev上个月在网上发布的一份证明中试图解决的问题。

现在,我们对“泡沫问题”稍作改变,只允许根据所谓的整数格(integer lattice)划分空间会怎样?
首先我们要知道什么是“格(lattice)”。在几何和群论中,实坐标空间R^n中的“格”是这个空间中无限个点的集合,具有这样的性质:格中两点的相加或相减会产生另一个格点,格点之间都间隔着某个最小距离,而且空间中的每个点都在一个格点的最大距离内。简单说,假如把空间里的向量的末端视为一个点,则格就是某空间里面的具有一些规律的离散的点集合,也可以说格是某空间中的一个离散的、具有加法运算的子群。

维空间中最简单的格就是整数格。整数格中最简单的就是基于笛卡尔坐标系的等基向量组成的空间。格在纯数学中有许多重要的应用,特别是在李代数、数论和群论方面。
回到问题,我们取一个等距点的方阵列(每个点间隔1个单位),并使每个格点成为形状的中心,就像这样:

现在的问题是,当以这种方式平铺空间时(格点必须在每个单元格的中心),最小的表面积将是多少?我们把这个问题称为“立方泡沫问题(Cubical Foams)”。这个问题可以帮助研究人员了解称为流形的拓扑空间的性质。
对于正方形情况,面积为1,周长为4:

正方形沿着网格平铺二维空间,但周长不是最小。
对于正六边形,面积为1,周长约为3.72:

正六边形以最小的周长平铺二维空间,但沿着一种不同的网格(不是整数格)。

对于非正六边形(choe's irregular hexagons),面积为1,周长约为3.86:
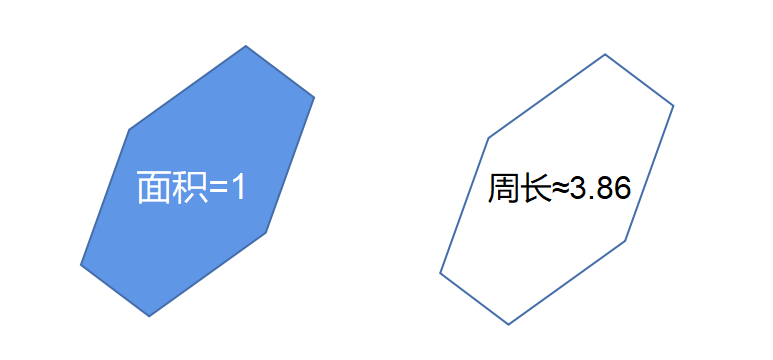
1989年,数学家Jaigyoung Choe证明了这些六边形在二维空间中沿着方格进行最佳平铺:

这在几何上也很有趣,因为它改变了"最优"的含义。例如,在二维空间中,如果正六边形只能在水平和垂直方向上移动整数个单位,那么它们就不能在平面上平铺。
正四边形可以。但这就是最好的方法吗?Jaigyoung Choe在1989年发现,最理想的形状是一个六边形,在一个方向上被压扁,在另一个方向上被拉长(当六边形的面积为1时,其周长约为3.86)。这些差异可能看起来微不足道,但在更高的维度上,它们会很明显。
在给定体积(二维空间是面积)的所有形状中,表面积(二维空间中是周长)最小的形状是球体(对应二维空间的圆)。随着维数n的增加,球体的表面积随着根号n成比例地增加。
但球体不可能在不留下缝隙的情况下平铺空间。而一个体积为1的n维立方体可以。问题是它的表面积是2n,与它的维度成正比。体积为1的1万维立方体的表面积为2万。
因此,研究人员想知道他们是否能找到一个“球形立方体(spherical cube)”——一种像立方体一样平铺n维空间的形状,但其表面积像球体一样增长缓慢。
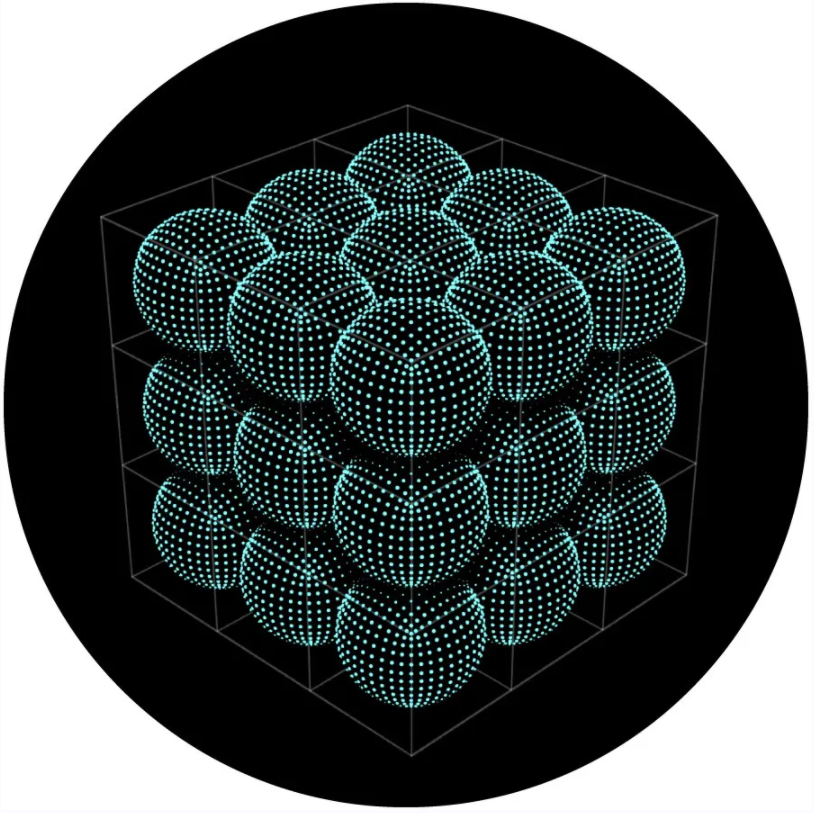
这似乎不太可能。
现在我们知道事实并非如此。难题的难度
难题的难度
几十年来,立方体泡沫问题(the cubical foam problem)在高维中相对未被探索。第一个在这方面取得进展的研究人员不是来自几何领域,而是来自理论计算机科学。当时计算机科学家正在寻找一种方法来证明计算机邻域领域中一个被称为UG 猜想(unique games conjecture)。UG 猜想是目前理论计算机科学中最大的悬而未决的问题。
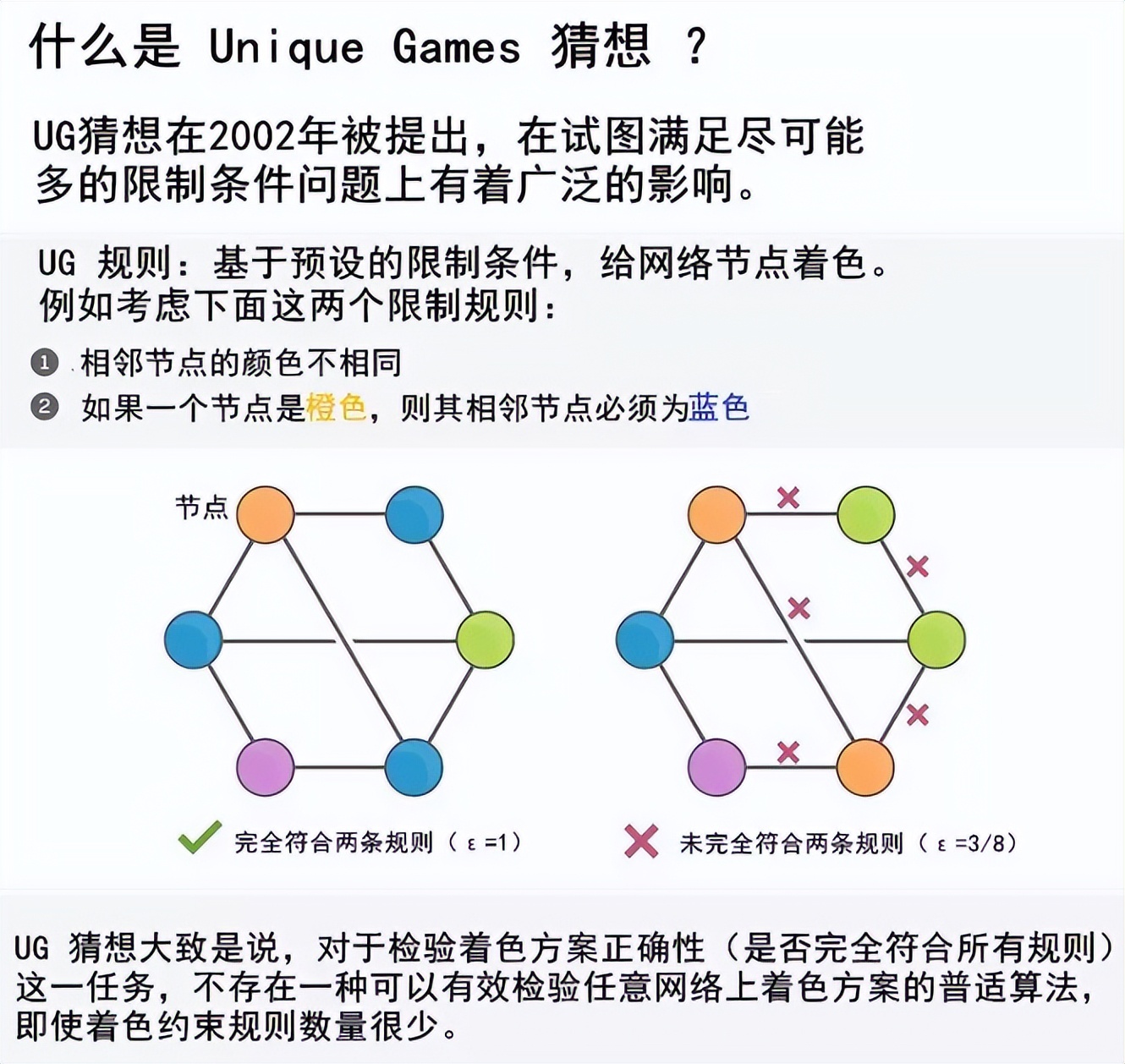
如果UG猜想是正确的,那么研究人员将能够一下子理解大量其他计算任务的复杂性。

数学家们认为,一种被称为Weaire-Phelan结构的形状以最小的表面积平铺三维空间。虽然他们还没有证明这一点,但物理实验为这一假设提供了支持。爱尔兰都柏林三一学院的研究人员在一个特殊的模具里装满了肥皂泡,发现肥皂泡自然地排列成Weaire-Phelan图案。
计算机科学家通常根据任务是否可以用有效的算法解决(或是否是NP难题)来对任务进行分类。例如,旅行推销员问题是NP难题(NPH),
旅行推销员问题说的是,假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
图着色问题也是NP难题。事实证明,要找到其中许多任务的近似解都是NP难题。
在UG猜想提出后不久,研究人员发现,如果猜想是正确的,那么可以很容易地计算出任何约束满足问题(constraint satisfaction problem)的难度阈值。因此,理论计算机科学家开始证明UG猜想,这项任务最终导致他们中的一些人发现了球形立方体。
把难题变得更难
2005年,O’Donnell等人联手解决了UG猜想问题。他们从一个关于图形的问题开始,就是所谓的最大切割问题(max-cut),当给定一个图时,如何将其顶点划分为两个集合,以使连接这两个集合的边的数量尽可能大。

如果UG猜想为真,这就意味着,给定一些随机图,一个有效的逼近算法只能得到该图真正最大切割的87%以内。如果想得到87%以上,就是NP难题了。
O 'Donnell走的是相反的方向:他希望证明最大切割是很难近似的,然后用它来证明UG猜想。他们的计划依赖于一种被称为平行重复(parallel repetition)的方法,一种让难题变得更难的方法。
假设你知道区分“一个你能解决的问题和一个你基本上可以解决的问题”是NP难题。平行重复可以让你在此基础上得到一个更难结果:区分一个你可以解决的问题和一个你几乎无法解决的问题也是NP难题。
但有一个问题。并行重复并不总是像计算机科学家希望的那样放大问题的难度。最大切割问题的某些方面“为平行重复制造了一个大麻烦。平行重复似乎有助于将最大裁剪与UG猜想联系起来。
首先,研究人员试图理解一个简单的最大切割情况下的平行重复。考虑由边连接的奇数个顶点形成一个环。

你想用两种颜色中的一种来标记每个顶点,使相邻的顶点的颜色不同。显然,这是不可能的,有一条边总是连接相同颜色的顶点。你必须删除那条边,以打破奇数环。最终,你想要最小化你需要删除的边的数量来正确地着色图形。
并行重复让你考虑这个问题的高维版本。在这个问题的高维版本中,你必须打破所有出现的奇数环。O 'Donnell需要证明,随着维度的数量变得非常大,你必须删除很大一部分边来打破所有的奇数环。如果这是真的,这将意味着并行重复可以有效地放大这个“最大切割”问题的难度。
然后,研究小组发现了一个奇怪的巧合,有一种几何方法来解释平行重复是否会像他们希望的那样工作。秘密在于立方体泡沫的表面积。
他们的问题,归结起来就是表明球形立方体不存在——不可能沿着整数格将高维空间划分成表面积比立方体小得多的单元格。正如计算机科学家希望的那样,更大的表面积对应着需要在奇循环图中删除更多边。
所以在2007年,他们发表了一篇论文,概述了他们计划如何利用这个问题来帮助攻击UG猜想。很快,他们的希望就破灭了。
普林斯顿大学的理论计算机科学家Ran Raz已经证明了几个关于平行重复的主要结果。他决定分析奇循环问题的平行重复。Raz证明了可以通过删除更少的边来打破图中的所有奇循环。换句话说,平行重复不能充分放大最大切割问题的难度。同时,Raz的结果也暗示了球形立方体的存在——能够平铺n维空间的形状,其表面积与n的平方根成正比。
2008年,研究人员证明了球形立方体确实是可能的。
这就引出了几何学方面的问题。球形立方体缺乏数学家喜欢的特性——形状更具体、更容易定义和研究、更适合潜在应用的特性。几何学有很大的潜力。只是我们还不够了解它。
评论列表