圆周率π的计算一直是数学界的一个热门话题。自从古代以来，人们一直在尝试用不同的方法计算π的值，这些方法包括使用几何学、无限级数、积分等等。目前，已知的π的十进制表示精确到了数千亿位，但是计算π的精确值仍然是一个挑战。

π出现在很多数学公式中，如三角函数、复数等等。π在几何学、物理学、天文学等领域中都有广泛的应用。本文将介绍5个非常著名且美丽的π公式。

π的莱布尼茨公式的形式是

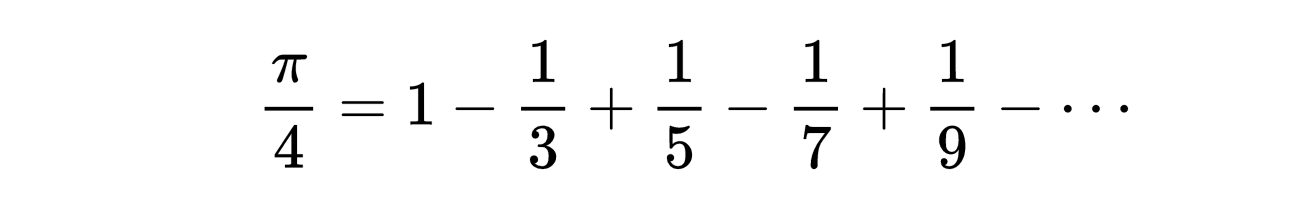
这个公式是由德国数学家莱布尼茨在17世纪提出的。这个级数是一个交错级数，也就是说它的每一项都是正负交替出现的。通过加上一些项，我们可以用这个级数来近似计算π/4，而随着项数的增加，我们可以得到更准确的近似值。

这个公式的证明可以使用数学归纳法和级数收敛定理。具体地，我们可以使用数学归纳法证明这个级数的前n项和是π/4的一个逼近值。然后，使用级数收敛定理可以证明这个级数收敛于π/4。

莱布尼茨公式是计算π的一种简单方法，但是它的收敛速度相对较慢，因此在实际计算中通常使用其他更有效的方法。

证明

有很多方法可以证明这一公式，例如，我们可以证明函数arctan(z)的泰勒级数是下面的幂级数

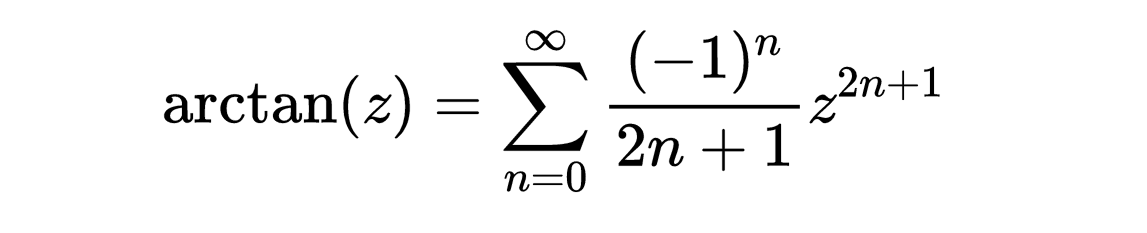
当-1≤z≤1时收敛。如果让z = 1，就能得到结果。所以，圆最终是藏在正弦和余弦的角度之间，因为我们最终要问的是，在哪个角度范围内（-π/2 ≤ θ ≤ π/2），使得sin(θ) = cos(θ)，答案是弧度为π/4。

1656年，约翰·沃利斯发表了π的沃利斯公式，指出π可以用以下无限积的形式给出。

证明

回想一下正弦函数的欧拉积公式，

令x = π/2，我们有

有时，这个结果可以用更简洁的方式来写出

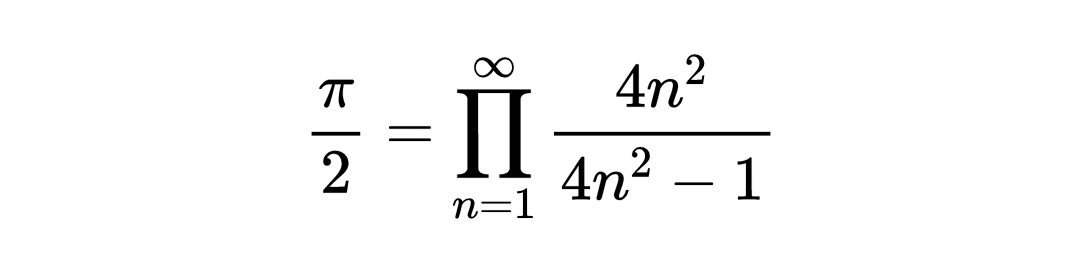
巴塞尔问题是一个著名的数学问题，也被称为巴塞尔（Basel）难题或巴塞尔和（Basel problem）。该问题最初由瑞士数学家Euler在1735年提出。

巴塞尔问题的具体内容是要求计算调和级数的和，即

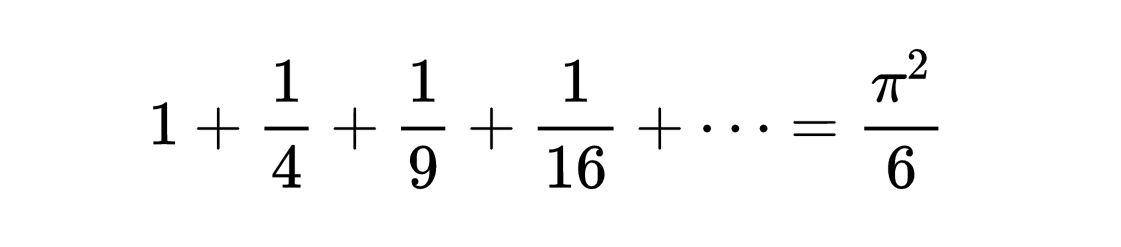
调和级数是一个无限级数，每一项是其下标的倒数。如果将前n项相加，可以得到一个有限的部分和。当n趋向于无穷大时，这个和会趋向于无穷大。然而，巴塞尔问题要求计算这个级数的无穷和，即所有项相加的结果。

这个结果的证明涉及到复变函数、级数收敛性、调和函数等数学知识，被认为是数学史上的一个经典结果。巴塞尔问题的解法也启发了许多其他数学问题的研究，如黎曼猜想等。

证明

下面的证明是欧拉自己提出的。回想一下，正弦函数的泰勒展开式是无穷级数

sin函数也可以写成无穷乘积，这个乘积需要一些证明，但欧拉确信这是可以的，所以他继续写

当然，作为欧拉，他很容易就看出了因子中的平方倒数，并想把它们提出来。他把乘积乘出来，得到

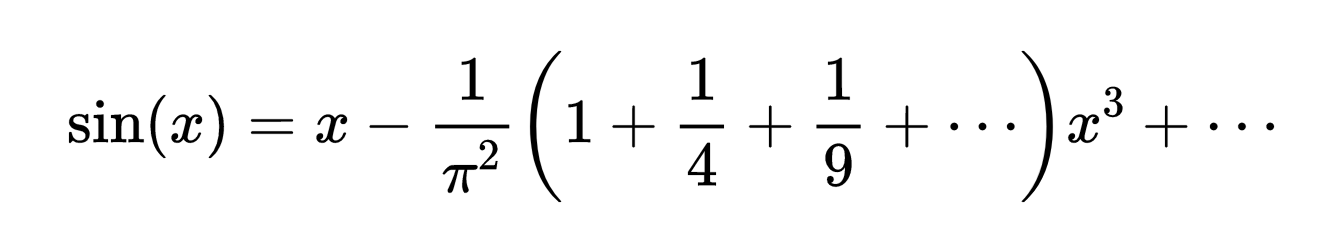
现在，这个幂级数表示必须和泰勒级数展开式完全相同，因此系数也必须相同。特别地，x^3项的系数必须相等。把这个等式写出来

布冯针问题的问题是：一根长度为L的针被随机地抛到一块地面上，这块地面上画有距离为d的平行线条，针与任意一条线的夹角θ随机取值，求针与任意一条线相交的概率。

解决这个问题需要使用概率论和几何学的知识。最终的答案是2L/(πd)。这个结果是概率论的经典问题之一，对于概率论和统计学的发展有很重要的意义。

布冯针问题也是一个典型的蒙特卡洛模拟问题，可以通过生成随机的针的位置和方向，计算针与线条相交的次数来估计概率。这种方法在实际应用中有着广泛的应用，例如计算圆周率、模拟随机过程等。

证明

为了简单和不失一般性，我们选择针的长度为1。想象一下，我们把平面放在笛卡尔坐标系上，把一条垂直线放在y轴上。然后，我们用x表示针沿x轴的中心位置，用θ表示交点的极限角，即，如果针和x轴的夹角在x轴的±θ范围内，则针位于垂直线上。它的图示是这样的：

如果针落在上图的灰色区域内，那么它将横过垂直线。考虑一下这个问题，我们实际上只需要一个参数，因为θ和x是因变量。特别地，三角函数cos(θ) = x。因为我们想把灰色区域写成x的函数，所以我们更愿意把θ写成x的函数，θ(x) = arccos(x)。

我们现在可以求出给定一个固定的中心x，即p(x) = 2θ(x)/π，针将穿过左边垂直线的概率。这是因为指针将始终在与x轴对应的左半圆的180度范围内，因此所有可能结果的空间是π弧度，而期望结果的空间是2θ弧度，对应于灰色区域。

但我们想要的是随机抛掷的针穿过任意一条线的概率。为了得到这个，我们简单地把从一条线到下一条线的无限多个可能中心对应的概率“加起来”。这是由积分给出的

因此，当随机抛掷时，针横在一条线上的概率正好是2/π≈0.6366，约为64%。

1901年，意大利数学家马里奥·拉扎里尼进行了布冯的针实验。他把一根针扔了3408次，得出了π的近似值355/113，精确到小数点后6位。

它是以伟大的德国数学家卡尔·弗里德里希·高斯的名字命名的。积分如下

它也被称作正态分布积分，可以被看作如下图中钟形图下的区域。

这个积分的解析式是不存在的，因此需要用一些特殊的方法来求解它。一个常见的方法是使用换元积分法结合对称性，将其转化为另一个已知的积分的形式。但使用极坐标的解更有启发性，因为它解释了π的存在。

证明

令这个积分的值为I，

对两边平方

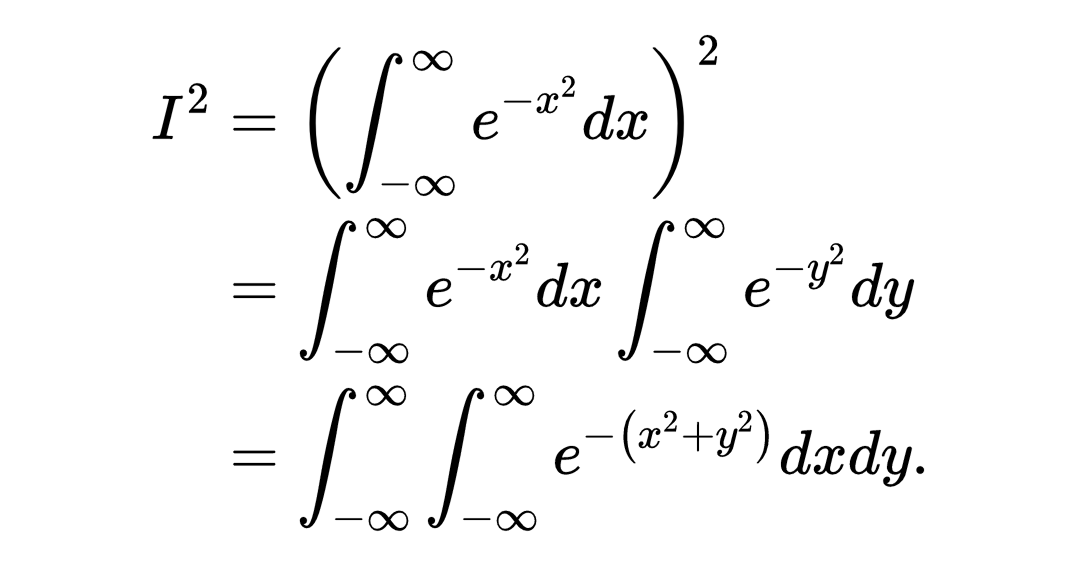
现在我们的问题是求出上面被积函数的二维图下的体积。注意，它在各个方向上都是旋转对称的

我们可以把它写在极坐标中，因为r^2= x^2+ y^2，r的范围是0到∞范围，θ在0到2π弧度范围内，因此

由于d/dr (-r²)= -2r，所以“逆”链式法则适用。因此我们得到

最后得到的结果是I^2= π。在这种情况下，π来自于二维高斯函数的旋转对称性，它是平行于xy平面的每一层的圆。