引用

Choi, Y., Lee, S., Won, J.. (2021). Learning from Nested Data with Ornstein Auto-Encoders. Proceedings of the 38th International Conference on Machine Learning, in Proceedings of Machine Learning Research 139:1943-1952 Available from https://proceedings.mlr.press/v139/choi21a.html.

摘要

许多现实世界的数据，例如 VGGFace2 数据集，它是一个由多个个体特征组成的集合，由于分组观察而产生了嵌套结构。Ornstein 自动编码器（OAE）是一个新兴的框架，用于从嵌套的数据中进行描述学习，基于随机过程之间的最优传输距离。OAE 的一个吸引人的特点是它能够产生嵌套在观察单元内的新变化，无论该单元是否为模型所知。以前提出的一个 OAE 算法，即随机截距 OAE（RIOAE），在学习嵌套表征方面表现出令人印象深刻的性能，但缺乏理论上的证明。在这项工作中，我们表明 RIOAE 最小化了所采用的最优传输距离的一个宽松的上界。在确定了 RIOAE 的几个问题后，我们提出了乘积空间 OAE（PSOAE），它能使距离的上界更小，并在表示空间中实现正交性。PSOAE 缓解了 RIOAE 的不稳定性，并为嵌套数据提供了更灵活的表示。我们证明了 PSOAE 在生成模型的三个关键任务中的高性能：范例生成、风格转移和新概念生成。

1 引言

许多现实世界的数据是在分组的观察单元中收集的。对于这样的嵌套数据，表征学习的目的是找到一个表征，在这个表征空间中，单元内的变化和单元间的变化被很好地分开。此外，该模型最好能处理未知的、可能是无限制的总观察单元数。同样，应该考虑到在一个单元内可以观察到无限制数量的变化。例如，在 VGGFace2 数据中，一个肖像的身份可以被视为一个观察单元。这些单元的数量可能是无限的，而可用的样本可能不包括所有的单元。一个单位的所有可能的变化也不可能被观察到。总而言之，我们需要一个可以采用各种嵌套结构的模型。

从表征学习模型获得的结构可以通过样本生成来证明。有三种类型的任务被提倡用来评估生成模型的质量：1）范例生成，生成给定观察单元的新变化；2）风格转移，将给定观察单元内的变化转移到另一个单元；3）新概念生成，相当于模拟新的观察单元；这可以与任务 1 和 2 相结合。对于这样的嵌套数据，一个适当的表示法应该是一个单一的表示法，它可以解决不限数量的观察单元和变化的所有三个任务。

为了获得一个能解决所有三个任务的单一表征，一个明智的方法是直接对潜在空间中的嵌套结构进行建模，并在它们之间找到适当的映射关系。

用 Choi & Won（2019）提出的算法训练的 OAE 在从 VGGFace2 数据中区分个体和从潜空间中高度不平衡的 MNIST 数据中区分数字方面表现出令人印象深刻的性能。OAE 的一个有趣的特点是，它可以从一个观察单元中生成样本，无论该单元是否存在于训练数据集中，甚至可以从潜空间中生成一个新单元。嵌套在一个给定的单元内，无论新旧，都可以生成具有新的变化或从其他已知单元转移过来的数据。然而，不幸的是，Choi & Won（2019）的算法所依据的一个理论主张被证明是不正确的，我们将在后文中看到。因此，他们的算法在实际表现和理论依据之间留下了一个耐人寻味的问题。

本文的目标是填补这一空白，并提供一种具有更好理论依据的改进型学习算法。我们首先表明，Choi & Won（2019）关于可交换过程之间的最佳运输距离减少为更简单的 Wasserstein 距离的说法是不正确的。然后我们表明，Choi & Won（2019）的算法实际上优化了最佳运输距离的上限，即 Ornstein 的 d-bar 距离。基于这一观察，我们继续推导出一个更严格的上界，并提出一个优化这一改进的上界的算法。这个新的约束还施加了一个明确的约束，即编码单位内和单位间变化的两个潜在变量应该是独立的，这在以前的方法中是缺乏的。由于这种分离，目前的 OAE 算法在所有三个学习任务中的表现都有很大的改善，在其他尝试失败的任务中也有明显的改善。

2 Ornstein 自动编码器

Ornstein 自动编码器（OAE）是一种 LVM（latent variable model，潜在变量模型），它采用 ρ-(PX,PY)来表示 D(PX,PY )，即 PX,PY 分布之间的偏差 D。它定义了一个具有先验分布 PZ 的潜伏随机过程 Z∈Z∞，并学习了一个确定性的解码器 g：Z∞→X∞，它将静止序列映射到静止序列，Y=g(Z)。

论文方程(3) (Choi & Won, 2019, 引理 1)这里，QZ|X 是条件分布（概率编码器）QZ|X 的集合，使得 QZ|X PX 在（X，Z）中是联合静止的，并且总后验 QZ QZ|X dPX 等于 PZ。通过对 g∈GN N 进行最小化（3），我们得到一个 OAE 模型。

3 随机截距 OAE

3.1 用于可交换数据的 OAE

最简单的情况是，当过程 X 和 Z 都是独立、分布均匀（以下称 i.i.d）时，OAE 提供了一个可操作的算法，在这种情况下，方程 3 简化为单个坐标之间 p-Wasserstein 距离的 p 次方。

受这种简化的驱动，Choi & Won (2019)声称，如果对过程{(Xj , Zj )}是可交换的，那么同样的简化是可能的。这一主张是可信的，因为 De Finetti 定理指出，可交换序列是以 i.i.d 为条件的。然而，他们的主张依赖于这样的假设：在 P (PX0 , PY0 )里的(X0 , Y0)的边际分布有这样的表示：∫F1dPF, 对于在 X×X 上的随机分布 F1 和它的分布 PF。除了真正的 i.i.d.序列，这在一般情况下是不成立的。

尽管缺乏理论支持，但在论文补充材料（算法 i）中复现的以供后续参考的 Choi & Won (2019) 算法显示出成功的结果。 下面的结果阐明了他们算法的理论依据，并且就其本身而言很重要，因为它根据过程的单个坐标提供了 ρ- (PX , g♯ PZ ) 的上限。 回想一下，De Finetti 定理 (Olshen, 1974) 的一个版本确保了当序列 X 是可交换的，实值随机变量的存在，以 X 的坐标为 i.i.d 为条件。

定理 3.1。假定 X∞ 上的过程分布 PX 和 Z∞ 上的 PZ 都是可交换的。还假设存在存在一个关于在另一个完整的、可分离的度量空间 B 上的分布 PB，使得其联合分布 PX,B 和 PZ,B 分别满足 PX1:n ,B =[P j =1n PX0 |B ]PB 和 PZ1:n ,B =[P j =1n PZ0 |B ]PB，对于任何 n。那么，对于任何可测 g : Z∞→ X∞，将一个可交换序列映射到一个可交换序列，我们有

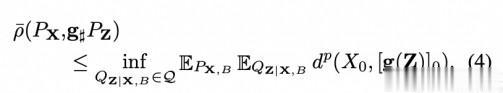
DOAE(PX,g♯PZ).为了使这个上界具有可操作性，1）需要知道对 X 和 Z 进行解卷的随机变量 B；2）需要解决解码器 g 的复杂性。后一个问题可以通过要求 g(Z)=（. . , g(Z-1), g(Z0), g(Z1), . . )，因为一些可测量的函数 g：Z→X。在这种情况下，稍微滥用一下符号，我们把 DOAE(PX,g♯PZ)写成

请注意，当 X 和 Z 都是 i.i.d.时，偏差（5）与偏差（3）重合，也就是说，OAE 还原为 Wasserstein 自动编码器(WAE，Tolstikhin et al., 2018)。

3.2 随机截距 OAE

为了解决上一段的第一个问题，算法 i 使用随机截距模型对 PZ 执行可交换性：对于给定的分布 PB 和 PE0，单元 i 的随机过程 Zi 和随机变量 Bi 的联合分布 PZ,B 被指定为

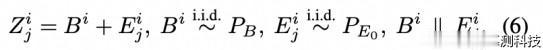
根据 De Fenetti 定理，有一个随机变量 Bˆ 对 X=d Xi 进行分解，即 X=（...，X-1，X0，X1，...）的坐标在给定 Bˆ 后是有条件的 i.i.d。那么 X 和 Bˆ 的联合分布 QX,Bˆ 具有 X-边际 PX。因此，条件分布 QBˆ |X 是定义明确的。理想情况下，为了满足定理 3.1 的假设，QX,Bˆ 的 Bˆ 边际应该等于 PB。因此，我们要求

并将 QBˆ|X 作为一个 "优化变量 "来学习。

为此，算法 i 可以被理解为解决以下优化问题

目标函数的第三项是约束条件（7）的惩罚形式。第二项是一个额外约束的惩罚形式

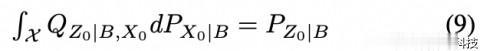
这与(7)一起促进了(QZ0|X0,B,QBˆ|X)对填充一个条件分布 Q ～ Z|X,B∈Q的集合Q～，其中后者的集合在定理 3.1 中定义。在这些约束条件下，第一项与方程（5）的 infimand 相吻合。下面的结果表明，Q～是Q的一个适当子集。

命题 3.1 假设 X∞ 上的过程分布 PX 是可交换的，随机变量 B∈Z 对 X 进行分解，因此 PX1:n ,B =[P j =1n PX0 |B ]PB，对于任何 n。给定 Z 上随机变量 E0 的分布 PE0，假设 PZ 的随机截距模型（6）。如果我们定义

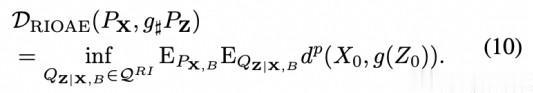
其中QRI 是条件分布 QZ|X,B 的集合，使得对于任何 n, (X,Z,B)的联合分布 PX,BQZ|X,B 在(X1:n,Z1:n,B)上具有边际[P j =1n QZ0 |X0,B]PX1:n,B，并且约束条件(9)成立。那么

因此，算法 i 最小化了(4)的右手边的上界，而这又是左手边的一个上界。由于这些原因，算法 i 所隐含的 LVM 可以被称为随机截距 OAE。

4 乘积空间 OAE

4.1 随机截距 OAE 的问题

目前对随机截距 OAE（RIOAE）的分析至少揭示了三个问题。首先，目标 DRIOAE(PX,g♯PZ)只是 DOAE(PX,g♯PZ)的一个上限，而 DOAE 已经是 ρ ̄(PX, g♯PZ)的一个上限（命题 3.1）。此外，约束条件(7)和(9)不够强，无法施加随机截距模型(6)的独立性和可加性要求，导致训练的不稳定性。最后，约束条件（9）是针对所有可能的观测单元，即针对所有可能的 B 值施加的。由于约束条件数量过多，必须有足够数量的观测数据，每个单元都有不同的变化，才能保证训练成功，这对现实世界的数据来说是一个特殊的特征。

4.2 潜在空间的乘积空间模型

随机截距模型（6）并不是对 Z∞ 中的序列 Z=（--,Z-1,Z0,Z1,--）施加交换性的唯一方法。更重要的是，这个模型的附加结构可能会限制整个生成模型的表达能力。一个更灵活的方法是将 Z 分解为 I×V。对于 I 上的给定分布 PB 和 V 上的给定分布 PE0，我们在 Z∞ 上指定 PZ 为

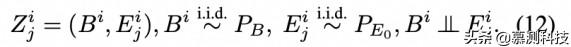
理想情况下，Bi 编码的是 Zi 坐标中共享的观察单元的 "身份"，即 Z 的第 i 个独立副本，Eji 编码的是所有观察单元中共享的 "单元内变化"。显然，Zi 是可交换的。此外，序列（...,g(Bi,Ei-1),g(Bi,Ei0),g(Bi,Ei1),...）对任何函数 g:I×V→X 来说都是可以交换的。（6）中的加性约束 Zji=Bi+Eji 被吸收到解码器 g 中，如果合适的话可以从数据中学习。我们称这种更灵活的 OAE 方法为乘积空间 OAE。

与 RIOAE 相比，乘积空间 OAE（PSOAE）的关键优势在于它直接优化了上界（5）

定理 4.1假设 X∞ 上的过程分布 PX 上的过程分布是可交换的，而 I 上的随机变量 B 分解 X，因此 PX1:n ,B =[P j =1n PX0 |B ]PB，对于任何 n。假设 Z∞ 上的过程分布 PZ 遵循乘积空间模型（12）。那么，对于解码器 g(Z)=(...,g(B,E-1),g(B,E0),g(B,E1),...) ，我们有

如果我们让（X0，B，E0）的联合分布为 QX0,B,E0=QE0|X0,BPX0,B，那么，给定 B 的 E0 的诱导条件分布是 QE0|B=QE0|X0,BdPX0|B。因此，定义QE0 集合的约束条件被写为

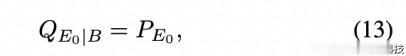
这意味着：1）E0 和 B 相对于 QX0,B,E0 来说是独立的，2）诱导的边际 QE0 等于给定的边际 PE0。后面的条件可以写成

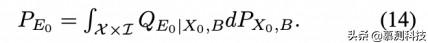
在定理 4.1 中 DOAE(PX, g♯PZ)的重新表述中，条件分布 PB|X 是未知的。与 RIOAE 一样，我们可以引入一个新的 "优化变量 "QBˆ|X 并施加约束（7）。

那么由此产生的 PSOAE 的优化问题是

对于适当的偏差 DB 和 DE0 的选择；最后的惩罚是衡量由 QX0,B,E0 引起的 B 和 E0 的联合分布的独立性的偏差。

备注 4.1 定理 4.1 中对 DOAE（5）的描述很重要，因为方程（13）到（15）显示，"身份 "潜变量 B 和 "变化 "潜变量 E 的贡献是明确独立的。这与基于 DRIOAE（10）的 RIOAE 形成鲜明对比，在 DRIOAE 中，这两个变量不是完全正交的。其含义是，在 RIOAE 训练期间，B 可能会吸收 E 的一些变化，导致不稳定（见第 4.1 节）。因此，新的约束 DOAE 的价值不仅限于对 DRIOAE 的紧密度（10）。目前还不清楚这样的特征是否也可以用 DRIOAE 来描述。

4.3 通过乘积空间 OAE 训练

交替优化。根据经验，以下坐标下降型交替优化方案在训练 PSOAE 时是有效的：1）固定 "单元内变化编码器 "QE0|B,X0 的参数，并更新 "身份编码器 "QB|X 和解码器 g 的参数，直到问题（15）的 infimand 不再变化。2) 固定身份编码器的参数并更新 QE0|B,X0 的参数和解码器 g 的参数，直到问题（15）的 infimand 不再改变。3) 重复步骤 1 和 2 ，直到编码器对(QB|X, QE0|B,X0)的参数和解码器 g 的参数趋于一致。与 RIOAE 类似，我们使用 DGAN 用于 DE0，DMMD,κ 用于 DB。训练程序被总结为算法 1。

初始化。在实践中，随机变量 B 只能分解输出过程 Y，而不一定是输入 X。理想情况下，潜伏变量 B 或其副本 Bˆ 应该对观察单元的实现进行编码，并使输入 X 的坐标成为有条件的 i.i.d.，因此，编码器 QBˆ|X 应该是某种平滑版本的分类器。训练数据的任何合理的分类器都可以被拟合并作为 QBˆ|X 的 "初始值"。例如，VGGFace2 可以采用预先训练好的 ResNet 分类器（Cao 等人，2018）的最后一个隐藏层的特征。

5 实验结果

对于 MNIST 数据，随机选择的 40,357 张图像被用于训练，其余的被用于测试。表 1 报告了对总体/少数/多数类的重建质量的几个衡量标准，在 100 个范例生成的 10 次重复中取平均值。(单次)准确性衡量的是 MNIST 训练的深度数字分类器对每个数字的五个(一个)生成的图像的分类准确性。用于计算分类准确率的分类器是一个具有 898k 参数的 CNN，用所有生成模型使用的通用训练数据进行训练。它用表 1 中用于计算数值的测试数据进行测试，并训练到其测试精度达到 0.994。

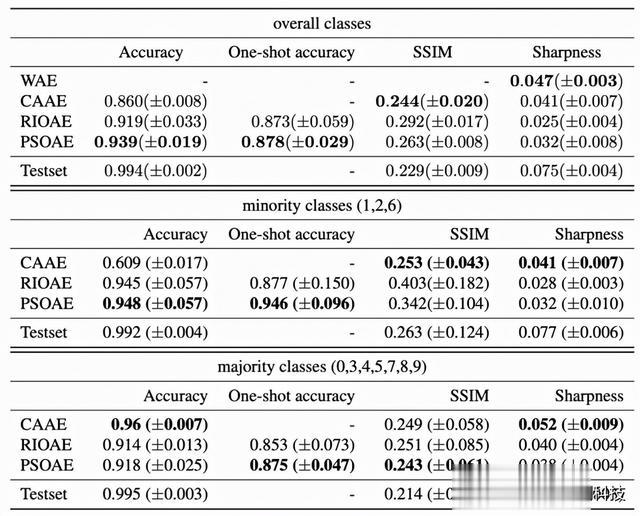
表 1 MNIST 性能测试结果

对于 VGGFace2 数据集，每张人脸图像都被裁剪并重新缩放为 128×128 像素的通用尺寸。训练集包括 2,513,512 张来自 8,631 人的图像。两个独立的测试集被用来测量性能。一个是由训练中使用的 8,631 人的 628,378 张图像组成。另一个测试集是由 500 个未包括在训练集中的人的 169,396 张图像组成。

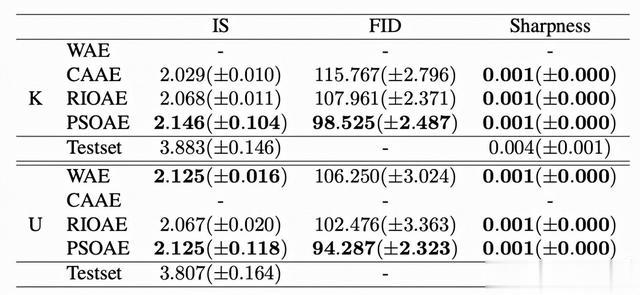
表 2 VCGFace2 性能测试结果

在表 2 中，一次范例生成的质量是由起始得分（IS）（Salimans 等人，2016）、生成图像的清晰度以及生成的图像分布与原始图像分布之间的 Frechet 起始距离（FID）（Heusel 等人，2017）来量化的。这些衡量标准是对 30 个范例生成的 10 次重复的平均数

6 结论

OAEs 是一个很有前途的新模型系列，当数据具有嵌套结构时，它可以学习分解表征。关键的吸引力在于它们能够为未知数量的观察单元和单元内的变化生成观察单元的保全样本。特别是，当数据表现出可交换性时，OAEs 产生了可操作的学习算法。我们已经表明，以前的 OAE 方法（RIOAE）实际上最小化了 Orstein's d-bar 距离的一个宽松的上界，这是静止过程之间的一个最佳传输距离。我们的方法，PSOAE，通过最小化一个更严格的上界，缓解了 RIOAE 的不稳定性，并成功地分离了表示空间中的单元内和单元间的变化。这种分离的力量在表征学习的三个关键任务中得到了体现：范例生成、风格转移和新概念生成，PSOAE 在这些任务中都表现出了良好的性能。

致谢

本文由南京大学软件学院 2021 级硕士黄志斌翻译转述，尹伊宁审核。