微积分在物理学中的桥梁作用

微积分在物理学中的桥梁作用

引言

科学与数学，这对古老而又神秘的伴侣，在人类追求真理的征途中始终互为指引。数学，特别是微积分，宛若一座跨越知识海洋的桥梁，连结着复杂现象与理性探索。本文力图揭示微积分如何在物理学的革命中发挥桥梁的作用。

微积分，这门悠扬的数学语言，不仅仅是学术领域中冰冷的符号和公式。它代表的是一种看似神奇、实则严谨的变换艺术，是解读自然界连续性之谜的钥匙。在物理学——特别是力学、电磁学、量子力学与广义相对论等领域中，微积分不断演绎着新的使命，揭开各式物理定律背后的深层逻辑。

通过本篇文章，我们将轻盈地跳跃在科学的云端，深入浅出地探索微积分与物理学之间的纽带。我们不仅仅是为了解答怎样的数学原理支持了诸如牛顿运动定律、麦克斯韦方程组乃至薛定谔方程的实效性，更是想打开一扇窗，通过这扇窗望见那些支撑现代科技、推动人类文明进步的创新应用。

本文的结构安排如下：首先我们将探讨微积分在类似经典力学这样的传统物理领域中所扮演的角色，进而讨论其在电磁学、量子力学中的革新意义，然后再梳理它在统计物理学与热力学中的精妙运用，并最终探讨它在理解引力与宇宙学中的基石作用。

从经典到现代，让我们共同见证微积分在物理现象与理论之间搭建起的桥梁，讨论它如何成为实现知识创新最为坚实的支持。

一、微积分：科学与数学的交汇点

核心概念概述

在数学的浩瀚领域里，微积分如同一条奔腾不息的河流，灌溉着科学的每一寸土地。微积分不只是关于变化的研究；它是变化背后秩序的解码者。这门学科从基础的导数与积分出发，延展至泰勒级数、微分方程乃至高级的拓扑与分析领域。

导数让我们能捕捉瞬间的变动趋势，积分让我们将这些微小的片段汇聚成完整的景象。在经典物理中，这意味着从一瞬间的加速度找到一段时间内的速度变化；在现代物理中，意味着从局部属性推导出整体的物质行为规律。微积分在物理学中的核心位置，源于它能准确描述自然界连续与动态的特性。

无论是在牛顿的经典力学中精确计算物体的运动，还是在麦克斯韦的电磁理论中探求电磁波的传播，抑或是在量子力学与广义相对论中探索微观粒子与宏大宇宙的奥秘，微积分都以其精确的语言赋予理论以数学的形式，建立起观测现象与理论预测之间稳固的桥梁。

在微积分这座牢固的桥梁上，物理学的许多重大发现纷纷起舞，奏响了人类认识世界的和谐乐章。而当我们抬头望向未来，数学与物理的紧密联系还将继续指导我们前往知识的新领域，解开更多待解之谜。

现代物理学的发展史纵览

从牛顿和莱布尼茨的无穷小的鬼魂，到今日大厦般稳固的理论：微积分不仅仅塑造了数学的面貌，更是在物理学史上留下了浓重一笔。我们的物理学之旅，是与微积分息息相关的——牛顿的“流数”(fluxions) 和莱布尼茨的微积分原理让自然界的规律首次被精确数学化。

探索微积分在物理学中的历史角色，就是回顾了物理学最辉煌的年代。从天体运行的简洁表达到热力学第二定律的形成，再到量子力学与广义相对论的开创，每个重大突破的背后，都伴随着微积分的崛起。

17世纪中期牛顿与莱布尼茨的独立工作揭开了微积分的序幕。牛顿利用微积分描述了万有引力定律，而莱布尼茨的符号体系至今被广泛使用。微积分的诞生，代表了科学理论向数学化的转变，它使得对自然现象的预测和控制变得可能。

在电磁学领域，麦克斯韦方程的构建同样离不开微积分的助力。这一组方程汇集了电荷、电流与电磁场之间复杂的相互作用，可以说是将电磁学提升到一个全新的高度。而到了20世纪，微积分在量子力学与相对论中的应用展示了它在解释微观世界和宇宙尺度现象中的强大能力。

正是微积分这一有力的工具，使物理科学家能精确不乏诗意地探索宇宙的奥秘。哪怕在今天的高能物理和天体物理研究中，当你深入暗物质的研讨，或是谋算黑洞的轨迹时，微积分依旧发挥着不可替代的作用。这是一场追求知识的旅程，微积分不断地为物理学发展史上的重要里程碑增砖加瓦。

二、经典力学与微积分的华丽舞蹈

运动学的数学诗篇

牛顿的苹果：微分方程与运动规律

有一个流传甚广的故事，牛顿在看到苹果坠地的那一刻，突然领悟到了引力定律。不管这个故事的真实性如何，一个不争的事实是——牛顿借助微积分，将自然界的动态规律用数学语言描绘得淋漓尽致。

在牛顿的《自然哲学的数学原理》中，微积分并非显而易见。然而，如果我们今日回顾牛顿的工作，不难发现他所构建的运动原理实际上是建立在微分方程的基础之上的。牛顿第二定律描述了力和物体加速度之间的关系，这里的加速度是速度 对时间 的导数，而速度 则是位移 对时间 的导数。这个定律实际上给出了关于物体运动的一个二阶微分方程。

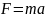
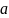
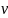
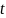
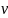
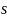
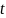
实例分析：行星运动与微积分

行星和其他天体的运动是经典力学中的一个典型案例。开普勒定律描述了行星运动的三个基本规律，而牛顿的万有引力定律则为这些规律提供了解释。在微积分的帮助下，这种看似复杂的天体运动现象能够被转化成数学上的轨迹问题。

以行星围绕太阳旋转的运动为例，可以通过求解牛顿定律中的微分方程来计算行星的轨道。这些方程不仅仅解释了天体为什么会沿着椭圆轨道运动，还能精确预测这些天体的位置。这一切都归功于微积分——物理规律与数学分析之间精妙的舞蹈。

动能与势能的微积分之旅

解密动能定理背后的积分原理

动能定理不仅是经典力学中的基本定理之一，更是微积分在物理中精妙应用的范例。这一定理告诉我们，物体的动能变化等于对其所做的功。在数学上，这表示为，其中是动能的变化，而 是对物体做的功。功的计算需要用到微积分中的积分运算，因为我们必须将力在位移方向上的分量与物体位移的矢量产品进行积分。

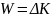
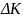
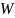
简单来说，当你推一块石头让它滑动时，你对石头做了功，这个过程涉及力和位移，而最终的能量会转化为石头的动能。利用微积分，我们能精确量化并计算出这一能量。

功-能定理与物理世界的无限可能

功-能定理是连接微积分与物理学的又一金桥。这一定理揭示了能量守恒原则，将力的概念与能量的概念紧密地联系了起来。它基于一个看似简单却深奥的微积分原理：力随位移的积分。这意味着物理学中非常复杂的运动和作用力问题都可以转化为可用数学积分解决的问题。

例如，考虑山谷中的一座水坝，水的势能转变为流出时的动能，这个过程可以通过积分动能和势能来详细描述。通过计算水从高处到低处滑落过程中的能量变化，我们能够用数学语言准确描述整个能量转化过程。

这些原理都是我们现代工业和科技成就的基石——从发电机到汽车引擎，甚至是人体内部的能量转化，处处可见动能与势能、微积分与物理交织的华丽舞蹈。

三、电磁学中的微积分精髓

麦克斯韦方程组的数学神秘

微分形式与积分形式的对比

19世纪后期，麦克斯韦方程组的普及开启了电磁学理论的新纪元。这些方程在表述上有两种形式：微分形式和积分形式。微分形式将电磁场描述为电荷和电流的局部分布，借助偏微分方程刻画电场和磁场的空间及时间变化。而积分形式则强调了电磁场与特定区域中的电荷和电流之间的全局关系，通常是通过环路积分和面积积分来表达。

微分形式的方程刻画了电场和磁场的点值行为，即在任意一点的精确表现。而积分形式则描述了电场和磁场在一定区域内的总体效应。

电磁波的产生与微积分

电磁波可以看作是麦克斯韦方程组的一个直接产物。电磁波的理论预测，是对麦克斯韦方程组的一个漂亮应用，将时间变化的电场和磁场联结在一起。在微积分的帮助下，麦克斯韦展示了怎样从一个振荡的电荷分布出发，推导出电磁波方程。

电磁波方程综合了微分形式的方程，将变化的电场与变化的磁场相关联，以波的形式在空间中传播。这一发现不仅证实了电场和磁场的波动性，还预言了无线电波、微波等电磁波的实际存在，开创了后来的无线通讯技术。

总的来说，电磁学中的微积分精髓在于它提供了一种方法，将物理量的局部变化与整体属性联系起来，使得我们可以精确计算出电磁场的行为，并预测与之相关的自然现象。微积分在这里再次发挥了桥梁的作用——它不单连接着数学与物理学，更连接着电磁学的理论与实践。

矢量场与标量场的秘密

探索电动力学的数学基础

在电动力学中，矢量场和标量场的概念是描述物理现实的基础。微积分提供了一组强大的工具来处理这些场。矢量场如电场和磁场，是通过空间每一点的矢量值来定义的，涵盖了方向和大小。而标量场如电势，仅通过每一点的数值来描述。

麦克斯韦方程组通过偏微分方程来表达这些场的动态变化，并且展示了电场和磁场如何相互作用和转化。比如，电场的旋度等于磁场随时间的变化率，而磁场的旋度则与电流密度加上电场随时间的变化率成正比。

图解：微积分揭示电磁场的结构

微积分不仅仅使我们能够处理电磁场的连续变化，还让我们能在可视化的图表中得到直观的认识。利用向量场的流线图，我们可以描绘出电场线和磁场线，看到它们如何环绕导体和电荷分布。

通过计算场线在特定区域的密集程度，微积分帮助我们量化场的强度。而电动力学中的环路定理和高斯定理，它们赋予了积分一个物理上的直观含义：环路积分使我们能绕着闭合路径测量电场或磁场的“旋涡”，高斯积分则使我们能量化闭合表面内的电通量或磁通量。

在微积分的映射下，电磁学的美妙结构一览无余。每一个数学推导都不再是枯燥无味的公式，而是赋予了电磁现象以形状和运动，将物理学的抽象理论转化为能与直观感觉接轨的具体图像。

四、量子奥秘与微积分的融合

薛定谔方程的数学之美

微积分在量子力学中的重要性

在量子力学的广阔舞台上，微积分无疑是主导的数学工具，其在理论构建中的重要性难以言喻。薛定谔方程，量子力学的核心之一，实际上是一个线性偏微分方程。这个方程形象地描绘了微观粒子的波动性，让我们得以探索电子与原子核间的错综复杂的交互作用。微积分在这里起到了翻译官的角色，将抽象的量子现象转化为具体的数学语言。

微积分在量子理论中的应用不仅限于薛定谔方程的求解，它还涉及到态叠加原理、不确定性原理等基本量子理论的建立和理解。微积分的工具，如傅立叶变换，成为解析量子系统的必不可少的手段。

量子跃迁与微积分的关系

量子跃迁，即量子态之间的突变，是量子力学中的一个飞跃。在微观世界中，粒子从一个能量级跃迁到另一个能量级所涉及的过程，可以通过薛定谔方程来描述。微积分在这里发挥的作用是对时间和空间的微小变化进行积分，以确定粒子状态的概率振幅。

更具体而言，当我们用波函数来描述量子系统时，波函数的平方为我们提供了找到粒子在某位置的概率。薛定谔方程提供了波函数随时间如何演化的细节，而微积分则为我们计算这些概率提供了方法。在理解和预测量子跃迁现象时，微积分不只是数学工具，更是连接理论与实验的纽带。

在量子物理的奇异世界中，微积分的应用范围广泛且至关重要。通过这个强大的数学工具，我们没入微观世界，揭露了万物运行的更深层次规律。微积分在量子力学中的应用，证实了它不仅是连接数学和物理的桥梁，更是一座通往宇宙深奥真相的桥梁。

测量与概率：微积分为量子界定规则

探索波函数与算符的关系

在量子力学的心脏——波函数的概念中，微积分扮演着至关重要的角色。波函数是一种数学工具，用来描述量子粒子在不同位置的概率振幅。一个粒子的波函数提供了一种手段，以数学语言精确描述其在量子层面的行为和特性。然而，波函数本身并不是直接可观测的量；它需要通过操作符作用来实现测量。

在量子力学中，物理量（如位置、动量、能量等）是通过算符表达的。算符作用在波函数上得到的结果，是对应的物理量的期望值或测量值。这种作用依赖于积分和微分——微积分的核心概念。例如，动量算符在一维空间中可以表达为，当它作用于波函数时，通过微分和积分运算，我们可以找到粒子动量的期望值。

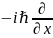
微积分在量子场理论中的应用

量子场理论在量子力学的基础上更进一步，它将粒子视为场的量子。在这个理论框架中，场被量化，粒子则从场的激发中产生。量子场理论的方程通常包含对时间和空间进行微分和积分的复杂数学表达式。

这里，微积分的作用不再局限于单个粒子的行为，它扩展到了描述无数粒子的集体动力学。微积分使我们能够理解和计算如粒子碰撞的过程，其中粒子的相互作用被视为场的叠加和干扰的结果。通过对场方程的积分和微分，物理学家能预测粒子如何在高能粒子加速器中发生相互作用。

在量子世界里，微积分不仅是数学的工具，更是理解和探索量子现象的重要钥匙。它使物理学家能够将抽象的量子理论转化为具体的可解方程，从而揭示物质的基本构造和宇宙的根本规律。

五、热力学与统计物理的微积分挑战

宏观现象背后的微观数学

统计力学中的配分函数与积分技巧

当宏观热力学遇上微观的统计力学，跨越尺度的桥梁便是配分函数（partition function）。这一关键数学概念涵盖了系统可能状态的全概率，并以此解释宏大热力学参数。配分函数的计算本质上是一个积分过程，它要求我们对系统可能的每一个微观状态进行求和（对于连续状态，则是积分）。这个过程揭示了整个系统的统计性质，并能从微观角度推导出熵、温度和压力等宏观量。

微观层面的各状态赋予的权重，例如在经典统计力学中，是通过能量、玻尔兹曼常数和温度 的指数因子 决定的。在量子统计力学中，这个积分过程更加复杂，但其基础——微积分——依旧是我们探索和计算宏观行为的工具。

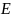
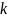
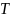
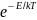
熵的微积分表达与演化

熵，作为热力学和统计物理学中最为核心的概念之一，其表达方式深刻地体现了微积分的力量。在熵的微积分表达中，我们不仅看到了几率分布的广泛应用，还见证了微积分如何量化复杂系统中无序度的增加。特别是，吉布斯熵公式将系统的熵与其态密度及概率分布联系起来。

在统计物理的框架下，熵以配分函数为起点，展现出系统发展的方向。随着状态的变化，熵的演化揭示了系统如何向热平衡转化，以及无法倒转的时间之箭如何在微观层面上被表达。

微积分在这一过程中不仅仅是一种计算技巧，更是一种让我们洞察整个物理世界的语言。当我们通过微观角度来理解宏观现象时，微积分便发挥了其真正的威力，让我们从数以无计的微小粒子的混沌中，抽丝剥茧地得到整个宇宙的运行规律。

相变与相空间的微积分

相空间理论与态函数的数学描述

在热力学和统计物理中，“相空间”是一个重要概念，模拟了系统所有可能微观状态的集合。在这里，每个点代表了系统的一个可能的状态，由诸如位置、动量等一系列变量的值决定。相空间理论让我们借助微积分工具——如偏导数和积分——将宏观量，如温度、压力和体积，和微观量联系起来。

态函数，如熵、内能和自由能，被数学地定义在相空间中，是相状态的函数。微积分不仅在定义这些态函数时发挥着关键作用，它还在描述相变——例如，从液态到气态——时显得尤为重要。例如，根据克劳修斯-克拉珀龙方程，微积分能帮助我们理解相变过程中温度和压力如何变化。

微积分在非平衡热力学的应用

非平衡热力学是研究远离平衡状态系统的学科。在这一领域内，微积分使我们能够研究和量化系统随时间的演化及其向平衡状态逼近的途径。其中，时间演化方程、输运方程等关键方程需要用到微分方程的积分技巧来求解。

例如，在描述传热或扩散等过程时，傅里叶定律和菲克定律等都依赖于偏微分方程。这些方程通过微积分技巧求解，能够预测热量和物质在不同介质中转移的速率和模式。

综上所述，在相变和相空间理论中，微积分不仅是数学的一种分支，它更是物理学理解自然的一把钥匙。无论是在描述静态的平衡状态，还是探索动态的演化过程，微积分都是热力学和统计物理中不可或缺的工具，它是物理学中的桥梁，连接了宏观现象与微观机制的世界。

六、广义相对论：时空几何与微积分的终极探索

引力的几何诠释与微积分

爱因斯坦场方程的数学骨架

爱因斯坦的广义相对论将引力理解为时空的几何性质，这是现代物理学中的一大突破。在这个理论中，微积分不仅是一种计算工具，更是一种深远的哲学思考。爱因斯坦场方程表现了物质如何告诉时空如何弯曲，而时空的弯曲又如何告诉物质如何移动。

场方程本身是一组复杂的非线性偏微分方程，它们描述了时空度量与物质内容之间的关系。在这里，度量张量描述了时空的几何结构，曲率张量则描述了时空的弯曲程度。求解这些方程需要高等微积分和微分几何的知识，方程的解即代表了在给定物质分布下时空结构的数学模型。

黑洞周围的时空弯曲与微分几何

广义相对论的一个著名解是描述黑洞的施瓦茨黑洞解。这个解揭示了当一个质量集中到足够小的体积时，所产生的时空弯曲如此之强，以至于就连光线也无法逃脱。描述这种极端弯曲的数学，需要使用到广义相对论中的微分几何工具。

在这个理论框架下，黑洞周围的时空不再是扁平的，而是弯曲的。黑洞的视界，或称为事件视界，是一个没有退路的边界，这个边界上时空的度量发生根本性的变化。要理解这种变化，就需要用到各种微积分工具，比如黎曼张量、黎曼曲率、测地线等概念。

广义相对论的美妙之处在于它将引力视为几何现象，而微积分正是探索这种时空几何的理想语言。通过对爱因斯坦场方程的钻研，我们不仅更深入地理解了时空的本质，也拓展了微积分在解释宇宙最基本力量中的应用。

宇宙学中的微积分应用

宇宙膨胀的数学模型

宇宙膨胀是现代宇宙学研究中的核心内容，其数学模型的建立和理解离不开微积分。广义相对论提供了一个强大的框架，其中爱因斯坦场方程描述了物质和能量如何影响时空的结构和演化。解决这些方程通常需要复杂的微分几何和偏微分方程技巧。

利用这些数学工具，科学家们建立了描述整个宇宙扩展历史的弗里德曼-勒梅特-罗伯逊-沃尔克（FLRW）度量。这种度量中微观分析清楚地表述了宇宙的动态特征，包括其尺度因子随时间的变化，即膨胀速率，这需要通过微积分中的积分和微分方程来求解。

辅助图表：解释宇宙大爆炸与微积分

宇宙大爆炸模型是描述宇宙早期快速膨胀状态的理论，它的建构也离不开微积分。微积分使得科学家能将观察到的宇宙背景辐射、星系红移等现象，用数学语言准确地表达在模型中，估计宇宙年龄、计算宇宙尺度因子的演变等。

通过辅助图表，例如宇宙的彭罗斯图和红移与距离关系图等，微积分不仅有助于科学家对宇宙演化做定量分析，更能帮助公众直观理解宇宙膨胀的概念。这些图表将复杂的宇宙学观念转换为具体图像，直观展示了时间和空间如何以一种非常独特和微妙的方式在宇宙尺度上协同工作。

结语

在这趟探索物理学中微积分应用的旅程结束时，我们清晰地看到，微积分无疑是现代物理学的基石。从最初引力定律的建立，到处理动态和静态场的复杂挑战，微积分始终是连接抽象概念与实际观测的桥梁。在处理连续性、变化和运动的基本原理时，微积分是物理学不可或缺的语言和工具。

未来，随着物理学理论的进一步发展，微积分的角色将持续扩展。不论是在量子引力、暗能量和暗物质的研究，还是在更为未知的天体和基本粒子领域，物理学家无疑还将继续依赖微积分去探索那些不为我们所知的领域。而微积分本身，作为数学与物理的桥梁，在未来的发展中，其核心原则也可能会随新发现而进化。但至少在可见的未来，它将继续作为解读世界的核心工具，成为我们理解宇宙的坚实基础。

随着数学技术的不断完善和新工具的开发，未来物理学家借助微积分解决问题的方式可能会有所不同，但微积分和物理学之间的深层联系将永远存在。这段不断发展的旅程不仅诠释了物理学的过去，也指明了未来的道路。让我们期待在不断推进的科学边界，微积分和物理学将共同绘制出未来充满惊奇的新篇章。

图文互动与读者参与

邀请解答与微积分有关的创意性难题：

难题一：行星运动的积分挑战描述一个简化模型，假如地球绕太阳的轨道是完美的圆形，通过使用牛顿第二定律和万有引力定律，结合微分方程来计算地球一年内绕太阳公转所描述的完整轨迹。

难题二：电磁场的变化之谜提供一个关于变化电磁场的问题，例如，探讨在一个改变的电场中产生磁场的过程。应用麦克斯韦方程中的法拉第电磁感应定律，利用积分找出一个时间变量的电场和它产生的磁场之间的关系。

难题三：量子概率的探寻给定一个量子粒子在潜能阱中的波函数，并要求读者利用波函数的归一化条件，使用积分计算，在特定区域内找到粒子的概率密度。

难题四：黑洞的广义相对论解邀请读者探讨在黑洞边缘，即所谓的事件视界处，空间和时间的行为如何变得奇异。这将涉及到对爱因斯坦场方程中的度量张量组件的积分和微分处理。

请投票选择下一个探讨主题

量子纠缠：揭秘量子世界的奇异联系如何即使相隔万里，量子粒子也能瞬间影响彼此？量子纠缠不仅挑战常识，也是量子计算和量子通信的基础。

暗物质的猎手：在宇宙中追寻不见之物暗物质至今无法直接观测，那么科学家如何确定它的存在？这将是一个关于宇宙中力量平衡的侦探故事。

宇宙的大尺度结构：从星系团到超级星系团我们的宇宙看起来是如何分布的？探索宇宙的大尺度结构，了解各种宇宙结构的分类法和形成机制。

量子计算机：超越经典计算的新时代量子计算机承诺将带来革命性的计算能力，但它们是如何运作的？我们将探讨其背后的物理和数学原理。

时间旅行：科学幻想还是未来可能？时间旅行一直激发着科幻小说家和物理学家的想象，现代物理学对时间旅行有何看法？

气候变化的物理学：解读地球的未来当我们讨论气候变化时，物理学可以为我们展示哪些关键证据和模型？

我们希望通过你的投票，了解哪个主题最触动大家的好奇心，那么就在评论区，让我们知道您的选择吧！您的参与，将直接影响我们下一步的冒险之旅！

电磁波理论是数学当物理，且隐藏了电磁以太假说，是不靠谱的经验公式。搞出两朵乌云，不能解释光电效应，都是对电磁理论的有效证伪，必须抛弃它(任何理论都是预测未来的全称命题，一个反例就足够证伪了)。依靠电磁理论，紫外灾难和其它更多荒唐结果，都是必然。………黑体辐射是轨道光粒子受激释放/激光，各个原子光谱线与各自“温度”对应，黑体辐射曲线峰值对应原子数量最多，紫外谱段原子数量很少，不奇怪。悖论斯坦不能拯救电磁以太，也不接受有效证伪，瞎搞成荒唐无源场，粒子搞成虚幻量子鬼，搞成波穿越真空，搞成波直线传播，搞成物质是运动(波)，搞成运动是物质，，，只能有更多笑话。

❌证实/证明理论是骗术：：：需要证明的真理/理论是骗，号称证明真理/理论也是骗！！！真理理论作为预测未来的全称命题，证伪当然有效，证明/证实当然无效。号称证明XX论和万有引力定律，都是骗。实验只能证明具体现象是真实。 认知自然/想知道能不能趟过一条河？没有经验知识无法演绎应用，创造假说也没用，只能依靠观测归纳。所有自然规律都是对过去的归纳，未来不变，不变的原因是不知道，只能信任自然！——“相对真理”也是骗术，真理是客观存在的绝对真理，人类诞生之前月亮不运动吗？？引力有没有？？都是显而易见！仰望星空信任自然的地心说需要认知进化，能否定绝对真理？？地心说依据的现象变了吗？没有！号称相对真理是悖论斯坦蔑视自然_欺师灭祖_搞骗的伎俩。❌❌大胆假设(规律)，细心求证，都是骗术，是悖论斯坦发家(科学家)的“两头骗”！用假设猜想后脑勺肯定没用，搞1000年可解释一切稀奇的鬼故事(假说假设，不是公设假定)也真不了，牛顿自然哲学反对任何创造假说！！！无人机，潜水艇，轮子，核弹的发明创造都是由公理和观测经验大胆演绎的结果/现象，与自然复杂现象一样，真理不变现象无穷多。质能方程演绎狗屎造核弹有用吗？

❌质能方程是一个鬼把戏！！！———能量的具体内涵是动能和势能，是物理公理规定的物理概念。物质质量是其不变的内在本质，能量(动能和势能)都是物质相互作用和相对运动变化的度量(质量不变)，是变化现象。能量不是物质的本质，咋能与孤立质量等效？？？场无质量居然有能量？………数学(包括逻辑)都是基于物理公理的演绎，超越物理公理的数学能量理解当然是虚幻(1+1=2是自然哲学/物理公理，牛顿定义自然哲学公理作为数学原理)。………🍎🍎物质的本质是带电质量体，物质不灭，电荷守恒，电磁力与万有引力统一于物质的不变本质。能量，力，场，波等宇宙一切自然现象，都是物质/粒子相互作用相对运动的变化现象，变化现象当本质(不变现象)是思维错乱丧心病狂。号称物质是波/波是物质/物质是能量，都是搞骗。质能等效是脱离基本公理的数学虚幻，欺师灭祖&蔑视自然，祸害基本概念和认知方法。——有人知道悖论斯坦的狗屁能量内涵是啥吗？……有趣的是木星象太阳一样自发光，它们的大气也相似。木星是裂变发光还是聚变发光？木星大气的氦和氢会不会是裂变反应释放的？满足聚变条件的太阳燃料喜欢缓慢燃烧吗？