修复量子理论核心致命缺陷的秘密可能隐藏在20世纪80年代让·埃卡勒（Jean Écalle）的三本晦涩的著作中。但物理学家们忽略了其中可能具有变革性的思想，因为书中充满了原创数学对象和奇特的用词。诸如“超级级数”、“可分析胚胎”、“异类导数”和“加速求和”这样古怪的术语比比皆是。而在这些数学中，可能包含了克服物理学上的一个困境所需的东西。

时至今日，物理学家已经学会对亚原子世界做出令人叹为观止的准确预测。但是，这些预测虽然精确，但只是近似值。如果寻求绝对精确度，教科书中的量子理论就会崩溃，产生无穷大的答案——许多物理学家认为这些答案是数学垃圾。

但现在，通过仔细研究那三本教材，物理学家发现了一种名为回升（resurgence）的数学理论。这一理论让物理学家意识到这些无穷大答案包含着无数宝藏，能让他们从任何无穷大中挖掘出任何量子问题的有限且无瑕疵的答案。

回升理论研究社群虽然规模较小，但多年来取得了稳步的进展。这个技术的原型版本在量子力学中已经获得了精确结果，而量子力学本身仅限于描述粒子的行为。更为复杂数学方法的发展使得一些物理学家能够深入探讨量子场论，甚至近期的弦论。然而，这只是回升理论实践者所怀有的宏大梦想的开始。他们的目标不仅仅是在物理理论中寻找一种全新的处理无穷大问题的方法，还希望这种方法能在理论和实践中更好地匹配我们的有限世界。

量子场论迫使物理学家直面无穷大问题。这些量子场是难以想象的复杂体系——在看似空无一物的空间中，瞬态波动和相干波动不断翻滚。从原则上讲，这些短暂波动可以在任何时刻、任何数量和任何能量下出现，这给物理学家带来了挑战，他们需要解释无尽的亚原子相互作用，以便理解甚至简单实验的精确结果。

在20世纪40年代，朝永振一郎（Shin'ichirō Tomonaga）、朱利安·施温格（Julian Schwinger）和理查德·费曼（Richard Feynman）都研究出了从量子电磁场的无穷复杂性中得出有限答案的等效方法。如今最为人所知的是费曼的方法，计算采用无穷多的“费曼图”来表示越来越复杂的量子可能性。首先从最简单的事件图开始（例如，电子穿过空间），并计算某个可测量的性质，比如电子在磁场中的摆动程度。接下来，将结果添加到更复杂的情景中，例如电子在飞行过程中短暂地释放然后再吸收一个光子。然后添加涉及两个瞬态波动的亚原子过程，然后是三个，依此类推，这种广泛应用的数学技术被称为微扰理论（perturbation theory）。

这种计算会产生一个无穷“幂级数”：

对于电磁场，x 的值是自然界的一个关键常数（即α），接近 1/137。这是一个相对较小的数字，适合表示力的相对弱度，将这个微小的数字提高到更大的幂使得各项迅速缩小。

费曼图为物理学家提供了每一项的系数——即a的值——这是计算中的难点。以电子的“g因子”为例，这是一个与粒子在磁场中摆动方式有关的数字。最简单的费曼图给出了 a_0，它恰好等于2。但是，如果考虑到稍微复杂一些的费曼图，比如第一个瞬态波动出现的情况，就需要计算 a_1 这一项，这也是无穷大开始出现的地方。朝永振一郎、施温格和费曼设计了一种使这一项有限的方法。他们计算得到的电子g因子约为2.002，这与当时的实验测量结果相符，证明了量子场论是有意义的，并使他们三人获得了1965年的诺贝尔物理学奖。

他们的方法也开启了一个新时代，在这个时代里，物理学家必须攀登越来越高的费曼图山，以便计算更多的a值。这些山很陡峭，增长得非常快。2017年，一位物理学家完成了长达20年的作品，精确计算了电子的g因子，这需要从891个费曼图中计算复杂的方程。结果仅揭示了该级数的第五项。

费曼图在现代物理学中仍然具有举足轻重的地位。一组类似但更复杂的计算用于μ子（电子的表亲），在2021年成为了头条新闻。一个实验显示，理论预测的结果与实际测量结果在第八位小数出现了差异。这个微小的异常现象代表着最好的希望，揭示了那些在费曼的工作基础上建立起来的巨大理论体系之外的未知领域。

然而，这一系列实验胜利掩盖了一个事实：从根本上讲，这种处理量子场论的方法实际上根本行不通。

弗里曼·戴森（Freeman Dyson），另一位物理学先驱，是第一位意识到微扰量子理论可能注定失败的物理学家。那时是1952年，当其他人庆祝费曼幂级数中的前几项可以变得又小又有限时，戴森开始担忧这个级数的其他部分。

物理学家天真地希望费曼图描述的电磁场处理方式会变成数学家所说的“收敛”。在收敛级数中，每个后续项都比前一个项小得多，项数越多，级数和越趋近于一个有限的数字。相反，级数也可能是“发散”的。发散的级数和是没有意义的。

费曼求和的前几项确实在缩小，这是因为α值很小，最初戴森得出的结论是微扰量子电磁学应该整体上是收敛的。

但后来，戴森将数学和物理推理相结合，对这个级数做出了更复杂的猜测。从数学的角度来看，戴森知道当x变得更小时，收敛幂级数收敛得更快，因为更高的项（涉及x的幂）收缩得更快。

但当他让x通过零时，一切都崩溃了。

原因与真空有关，真空不断产生瞬态的正负电荷波动对。这些波动通常相互吸引并消失。但如果α变为负数，这些波动会互相推开并变成真实的粒子。从无中不断涌现出的粒子会触发宇宙崩溃，正如戴森所说的“真空的爆炸性瓦解”。

从物理角度看，任何负α都会带来问题。然而，在数学上，x 的符号并不重要：如果一个级数在较小的负x值时发散，那么在较小的正x值时也应该发散。因此，对于较小的正α（即1/137），这个级数也应该发散。戴森的灾难性物理情景意味着费曼处理量子电磁学的著名方法最终预测出无穷大。

一个无法驾驭的无穷大。物理学家通常通过无穷求和来研究量子场，比如电磁场。这些求和中的前几项越来越小，为我们提供了一个近似答案。然而，后面的项会激增，导致求和看似失去了意义。

如今，物理学家预计量子电动力学（即电磁学的量子场论）可能在第137项附近开始发散。也就是说，

将其纳入求和会使预测的精度降低，而不是提高。

问题在于，更高的项会导致费曼图数量呈阶乘式的爆炸性增长。这意味着计算 a_9 大约需要 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1（约 362,880）个费曼图，而计算 a_10 则需要大约 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1（3,628,800）个费曼图。这种对 a 项贡献的费曼图数量的阶乘式增长速度最终会超越 α 幂次的缩小速度，从而使求和无法遏制地朝着无穷大增长。

对大多数物理学家来说，即使是最简单的量子场论的不可避免发散仍然是一个抽象问题。在计算（更不用说测试）这个级数的第10项似乎都像科幻小说一样时，为什么要担心远在100项之外潜伏的危险？

但对于少数物理学家来说，现代物理学中最为人们所理解的理论在技术上对任何问题给出无穷的答案仍然令人深感不安。即使原则上拥有无限的计算资源，我们也不知道如何模拟世界。

与此同时，数学家在戴森开始担忧量子理论之前的一个多世纪里，一直在思考发散级数。“发散级数是恶魔的发明，用它们来证明任何东西都是可耻的，”阿贝尔在1828年说。

阿贝尔在次年去世，享年26岁。但在世纪末，亨利·庞加莱朝着理解发散级数如此棘手的原因迈出了重要一步：它们并非恶魔般的邪恶，只是不完整。

庞加莱在探讨一个古老的问题：三个天体如何相互围绕运行？他试图用微扰理论来解决这个问题，正如费曼和戴森在一个世纪后遇到量子场时所做的那样。庞加莱试图用一个无穷长的简单单位之和来构建描述三个天体轨迹的复杂函数。人们希望这个级数收敛到一个有限的答案。

起初，他认为自己成功了。1890年，瑞典和挪威国王奥斯卡二世为庞加莱在这个著名问题上的进展颁发了奖项。但就在他的著作即将出版之前，他要求停止印刷。这个级数是发散的。进一步的分析（为混沌理论奠定基础）揭示出它匹配的不是一个而是两个不同的函数。如今，物理学家知道三个天体可以以无数种非常不同的方式相互作用，而没有简单的方程可以包含所有可能性。

圣路易斯华盛顿大学的数学物理学家卡尔·本德，将庞加莱遇到的那种发散级数比喻为函数的模糊视图。模糊包含许多可能的函数。当你将一个复杂的函数展开成这样一个“渐近”级数时，“你已经丢失了信息，”本德尔说。

自庞加莱时代以来，数学家和物理学家已经意识到还有其他类型的项，这些项是“超越所有阶”的，它们比最小的幂项还要小。这些“指数级小”的项可以采用 e^(−1/x) 的形式，例如，它们提供了丢失的信息。如果将它们包含在级数中，并采用合适的“重新求和”方法使级数变为有限，你就可以减轻部分（甚至可能是全部）的模糊程度。

物理学家称这些额外的项为“非微扰项”，因为它们超出了微扰理论的范围。你可以花上万亿年来画费曼图并计算a项，但你永远无法了解到这些非微扰项中所包含的某些物理事件。尽管这些微小项描述的影响可能很少见或微妙，但它们在现实世界中可能产生巨大的差异。

以量子力学的薛定谔方程为例，它描述了粒子的波动行为。这是一个复杂的方程，物理学家通常使用微扰理论对其进行近似。尽管所得到的无穷级数非常精确地预测了许多实验，但它完全忽略了一种极不可能（但不是不可能）的事件，即隧穿效应（tunneling）。在这种事件中，粒子穿越障碍进行了瞬间传输。

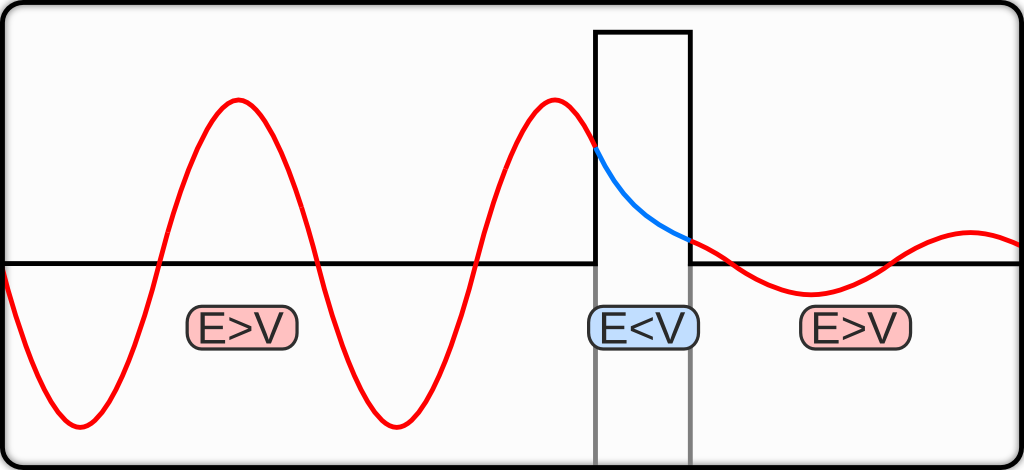
隧穿效应是量子物理中许多非微扰现象之一，但非微扰效应无处不在：雪花的分支状生长、液体通过带孔管道的流动、太阳系内行星的轨道、围绕圆形岛屿间的波浪涟漪，以及其他无数物理现象都是非微扰的。它们确实存在，而且至关重要，单纯依靠微扰理论是不够的。

由于非微扰现象具有普遍性，大量的数学家和物理学家致力于研究如何计算非微扰项这一问题。在20世纪末，一批研究人员开始发现一些引人入胜的线索，这些线索表明微扰级数似乎包含了比预期更多的信息。

在这些研究人员中，1980年代，法国萨克雷核研究中心的一个小组发展了一种将微扰幂项与非微扰指数项相结合的方法，以获得量子力学隧穿效应的精确结果。他们的技术在依赖一个称为波雷尔重求和（Borel resummation）的关键数学技术方面取得了成功。波雷尔重求和是当时从发散级数中得到有限数字的最强大工具，但它也有其局限性。它偶尔会给出错误，这让希望一个级数能正确预测某个实验结果的物理学家感到沮丧。

当物理学家发现一个无法用波雷尔求和的级数时，他们基本上就放弃了。他们不知道的是，一个离萨克雷小组只有几英里之遥的古怪数学家已经开始了对渐近级数前所未有的探索。

在20世纪70年代初，埃卡勒的好奇心驱使他步入了庞加莱的足迹。他开始分析在天体研究中出现的更抽象的数学对象。渐近级数逐渐出现，而他在高中时曾推测过的更通用导数也出现了。埃卡勒最终开发了他所描述的“一种精确、轮廓分明的结构——异类微积分（alien calculus），从发散中自发产生。”

埃卡勒的异类微积分抽象且多面。但对于物理学家来说，它传递的信息非常清晰。微扰级数，尽管发散，却隐藏了一整套非微扰信息。级数包含了所有升级所需的内容，以消除模糊并恢复与唯一对应函数的清晰图像。

尽管具有深远影响，但一开始，埃卡勒的工作并未受到重视。它对于物理学家来说太过晦涩和抽象，而对于数学家来说，它又不够严谨。

埃卡勒于1976年首次在三篇论文中勾勒出回升理论的核心概念，并在1981年至1985年间撰写了他的三本教科书，其中详细介绍了回归理论的异类微积分。这些教材从未在数学期刊上发表。

如果物理学家当时就开始研究他的书籍，他们的经历可能如同与拥有高度智慧的外星文明接触一样。他们将遇到远超他们习惯的数学工具。

当埃卡勒被《Quanta Magazine》联系并就回升理论的历史提问时，他花了六天时间撰写了一篇关于该主题的24页专论，这对于渴望了解有关回升理论及其发展的更多信息的研究人员来说是一件难得的瑰宝。

下面是这种方法的一个非常粗略的简化版：

首先，写出典型的微扰级数。一开始项会缩小，但最终随着a值变得非常大，它们会迅速增长。绘制a值的增长情况，你会看到它们向上增长的速度几乎与阶乘增长一样。研究a值描绘的线和阶乘增长曲线之间的差异，以了解第一个非微扰项。

不过，这只是开始。应用波雷尔重求和的第一步。这消除了阶乘增长，使你能更详细地看到微扰项的行为。经过修改的a的结果图应呈指数增长。但仔细研究它，你会发现微扰数据有些偏离。这个偏差来自于一个全新的渐近级数，你需要将其乘以第一个非微扰项。

这个过程继续。从微扰数据中去除指数增长，如果你观察得够仔细，你可能会发现进一步的偏差，这些偏差揭示了第二个非微扰项。再仔细看，你会发现这个非微扰项还伴随着另一个渐近级数。

最终，可能会有任意数量的非微扰项，每个项都附带一个渐近级数。找到尽可能多的这类项，你手中就会有一个称为跨级数的对象。跨级数从熟悉的微扰级数开始，然后是一个非微扰项（带有一个级数），接着是另一个非微扰项，依此类推。

埃卡勒的跨级数克服了之前困扰物理学家的波雷尔重求和的困难。如果你知道描述某个测量（例如电子的g因子）的跨级数，波雷尔重求和将给你一个唯一、正确的答案。此外，回升理论断言，跨级数开头熟悉的微扰级数中的微妙偏差会告诉你接下来可能无限的级数所需了解的一切。

这个数学图景对物理学家有两个引人注目的影响。首先，它暗示量子场和其他复杂系统可能存在精确结果——而不仅仅是近似。如果是这样，它将使量子理论成为有限且合理的。这将是一个重大的进步。

其次，这暗示着可能无限多的非微扰部分完全可以从微扰级数中推导出来，而微扰级数的发散困扰了戴森。几十年来看似独立的物理领域实际上是密切相关的。

埃卡勒的发现（通过微扰理论可以获取非微扰知识），已经逐渐渗透到数学物理世界。在这里，物理学家已经利用它在21世纪最受密切研究的两个理论中找到了隐藏的新部分：强力理论和弦理论。强力将夸克聚合在一起形成质子和其他粒子

北卡罗来纳州立大学的物理学家Mithat Ünsal，致力于研究强力。2008年，他在一篇关于发散级数的文章中阅读了关于回升理论的内容后，寻求了解埃卡勒的工作。后来，他在一次会议上遇到了康涅狄格大学的Gerald Dunne，聊天时，他们发现同一篇文章激发了他们两人开始自学回升理论。他们决定联合起来。

这两位物理学家的动力来自于他们试图理解比戴森和费曼面临的问题更复杂的事物。这些物理学家在电磁场方面很幸运。电磁场非常微弱，α只有1/137。另一个基本力量，弱相互作用，同样容易处理。对于这两种力量，微扰理论之所以有效，是因为它们非常微弱，几乎可以说它们根本不存在。

但是，当物理学家尝试解决强力时，这种运气就结束了。强力比电磁力大约强100倍，其α类似物约为1，不容忽视。平方或立方1根本不会产生任何缩小效果，因此微扰级数从最早的项开始就直接走向无穷大。物理学家花了几十年时间使用超级计算机开发一种处理强力的替代方法，并在此过程中取得了惊人的成果。但是，数值计算并不能很好地解释强力如何发挥作用。

Ünsal和Dunne认识到，具有驯服发散级数能力的回升理论可能会让他们朝着解强力的梦想迈出一步。特别是，他们着手解决困扰强力理论40年的一个谜团。

1979年，物理学家杰拉德·霍夫特和帕里西推断出强力计算中存在微小而奇异的项。他们称之为重整子（renormalons），没有人知道如何处理它们。重整子似乎与具体的场行为没有任何对应关系。但是它们确实在那里，不管怎样还是破坏了计算。

Ünsal和Dunne用回升来解决重整子问题。尽管他们研究的是强力的2D类似物，但这大约花了他们一年时间。但是在2012年，他们证明了至少在他们的简化模型中，霍夫特和帕里西的重整子与物理学家理解的行为相匹配。

然而，去年研究人员利用回升增加了进一步的复杂性。日内瓦大学的数学物理学家马里诺和他的合作者进行了更严格的计算（尽管也是在简化的理论中），并发现了新的重整子。马里诺现在怀疑重整子只是非微扰冰山的一角。如果他是对的，量子世界有一天可能会比现在更难以想象。

马里诺还在发现弦理论中一种新的非微扰效应方面扮演了关键角色，这种推测性认为宇宙不是由类似点的粒子组成，而是由扩展物体（如弦）组成。这种弦的振动将决定我们观察到的粒子的性质。

弦理论与量子理论一样，通常被视为一种微扰级数，用类似费曼的图表示弦以越来越复杂的方式合并和分裂。然而，与量子理论家不同的是，弦理论家甚至对理论中的非微扰效应也缺乏最基本的指导。他们认为，就像量子理论包含隧穿和重整子一样，弦理论的完全非微扰公式也包含未知的物理现象。

弦理论中一个引人注目的非微扰现象实例是在20世纪90年代发现的类似薄片的物体，称为D-膜（D-branes）。D-膜后来将推动弦理论的一些最大发展。

2010年，马里诺注意到在D-膜项的阴影中隐藏着一系列负相对物。目前还不清楚这些伴随项可能描述什么物理现象。

六年后，哈佛大学的卡朗·瓦法及其合作者在探索一个推广的弦理论时发现了线索，该弦理论中某些量可以为负数。他们发现了具有负张力的D-膜 —— 这是具有负质量的膜版本。这些奇异的东西扭曲了它们周围现实的结构，创造出多个时间维度并违反了概率总和必须为100%的基本原则。但该小组没有发现这些物体应该从它们的怪异世界逃脱，进入标准弦论。

现在，里斯本大学理论物理学家里卡多·斯基亚帕（Ricardo Schiappa）认为他找到了证据。最近几个月，斯基亚帕和他的合作者使用回升法仔细审查了几个简单的弦论模型。他们发现，瓦法的负张力D-膜与马里诺在2010年发现的指数级小项完全匹配。

其他理论家还不确定如何看待这个新发现。瓦法指出，斯基亚帕的团队在简化的弦模型中进行了他们的计算，该结果不能保证在更复杂的表述中成立。但是，如果它确实成立，而且弦论确实描述了我们的宇宙，那么它必须包含另一种阻止负D-膜形成的方法。

尽管物理学家在发现重整化子和负膜方面取得了进展，但他们认为，要将回升理论封为微扰理论的正式继任者，还有两个巨大的障碍。

首先，并非所有理论都被证明具有回升结构。对于量子场理论，这个问题尤为严重，物理学家一直在逐案检查。这是一个繁琐的过程。

这就是为什么Serone在过去三年里致力于在某些量子场理论中对回升法进行压力测试。2021年，他和他的合作者研究了一个与强力共享关键特征的理论，但仍然足够简单，可以让他们计算执行回升法所需的许多a。他们使用回升法和另外两种方法计算了这样一个宇宙中空间的能量，证明了这三种方法是一致的。有关回升法应该适用于量子场理论的定性论证，但这是首次具体计算之一，进一步激发了乐观情绪。

更严重的问题是，要发现非微扰部分，你需要知道大量的微扰项。例如，在他最近的研究中，Serone选择了量子场理论，让他生成数千个项。但对于强力，目前计算仅8或9个项是不可能的。即使是该方法的先驱们也不掩饰他们期望看到它产生一个实数（如质子质量）的时候（这是一个价值百万美元奖金的数学壮举）。

然而，艰巨的困难并没有扼杀从回归法中得到真实预测的梦想。首先，这种技术已经在量子力学中产生了其他无法获得的结果。早在20世纪80年代，法国的数学物理学家使用原始的回升法对粒子隧穿进行了精确预测，而这是物理学家之前只能近似的问题。另一组人使用标准方法检查了这些结果。他们只能达到六位小数点，这是一项耗时数月且需要相当计算能力的艰巨工作。

这些戏剧性的例子激励了Dunne努力开发高效的回升法实践方法，希望有朝一日将其用于量子场理论。在过去的五年里，他与俄亥俄州立大学的数学家Ovidiu Costin一起找到了可以在微扰理论中发挥更大作用的技术。在某些情况下（尽管距离现实世界的理论还很远），他们发现只需要10到15个项就足够了。

对于埃卡勒来说，回升法是过去的一个篇章。自他的原始三部曲以来，已经过去了近40年。过去20年里，他一直在研究一种更具代数性质的分支。如果他决定出版一个续集三部曲，在一个地方收集他所有的发现，谁知道物理学家会在其中发现什么宝藏。