行测题库｜数量关系｜每日一练：数学运算67

例题1

某市徒步协会组织了一项“清洁海岸线”公益活动。志愿者早上7点从市区集合出发。徒步前往市郊海岸线起点，然后沿海岸线捡拾垃圾。到达海岸线终点后立即沿原路折返。下午1点到达集合点一起收垃圾，已知志愿者正常的徒步速度为8km/h，捡拾垃圾的徒步速度为4km/h，返程负重的徒步速度为6km/h。去程与返程所用时间相同，则该段海岸线长（）km。

A.4

B.6

C.12

D.18

解析：

从早晨7点到中午1点，共6小时。

根据“去程与返程所用时间相同”，可知：往返各3小时。

根据“返程负重的徒步速度为6km/h”，可知：单程为6×3＝18km。

设海岸线长x千米，则集合点到海岸线长（18－x）千米。

根据“志愿者正常的徒步速度为8km/h，捡拾垃圾的徒步速度为4km/h”，可列方程：

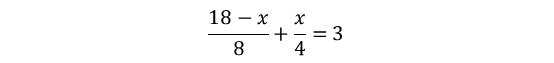
解得x＝6。因此该段海岸线长6km。

因此，选择B选项。

例题2

某工程50人进行施工。如果连续施工20天，每天工作10小时，正好按期完成。但施工过程中遭遇原料短缺，有5天时间无法施工，工期还剩8天时，工程队增派15人并加班施工。若工程队想按期完成，则平均每天需工作（）小时。

A.12.5

B.11

C.13.5

D.11.5

解析：

赋值每人每小时的工作效率为1。

根据“50人进行施工，连续施工20天，每天工作10小时，正好按期完成”，可知：工程总量为50×1×20×10＝10000。

根据“有5天时间无法施工，工期还剩8天时，工程队增派15人并加班施工”，可知：前20－8－5＝7（天）有50人施工。后8天有50+15=65人施工。

设平均每天工作t小时。

根据“总量不变”，可列方程：7×50×10＋8×65t＝10000。

解得t＝12.5。

因此，选择A选项。

例题3

将一叠文件分为若干组，每组正好有10份文件。已知其中2组文件中有18份通知，其余每组文件中最多有5份通知，且所有文件中通知占比正好为60%。那么这叠文件最多可能有多少份?

A.50

B.60

C.70

D.80

解析：

根据“这叠文件最多可能有多少份”，问“最多”，从D项代入：

因此，选择D选项。

例题4

为增强职工的锻炼意识，某单位举行了踢毽子比赛，比赛时长为1分钟。参加比赛的职工平均每人踢了76个，已知每人至少踢了70个，并且其中一人88个，如果不把该职工计算在内，那么平均每人踢了74个。则踢得最快的职工最多踢了多少个？

A.88

B.90

C.92

D.94

解析：

设职工共有x人。

根据题意可列方程：76x＝74（x－1）＋88。

解得x＝7。

共踢了76×7＝532（个）。

若要踢得最快的职工踢得最多，则其他职工踢得尽可能少。设最快的职工最多可以踢y个。

根据“每人至少踢了70个，其中一人88个”，可知：除去踢88个的那名员工，其他5名员工尽可能少，均为70个。

可列方程：532＝y＋88＋70×5。

解得y＝94＞88。

因此，选择D选项。

例题5

某商场促销，晚上八点以后全场商品在原来折扣基础上再打9.5折，付款时满400元再减100元。已知某鞋柜全场8.5折，某人晚上九点多去该鞋柜买了一双鞋，花了384.5元，问这双鞋的原价为多少钱？

A.550元

B.600元

C.650元

D.700元

解析：

假设这双鞋付款时已满400元。

根据“全场8.5折，再打9.5折，付款时满400元再减100元”，可知：这双鞋的原价为（384.5+100）÷0.95÷0.85=600（元）。

因此，选择B选项。