大家好，我是科学羊，这里是数学篇第五季第43篇。

鸽巢原理，也被称为“抽屉原理”，或狄利克雷抽屉原理，是数学中一个非常基础且常见的概念。

它听起来可能非常简单，甚至有点儿显而易见——如果有多于n个物体要放进n个容器里，而每个容器只能容纳一个物体，那么必然至少有一个容器里会装有多个物体。

这种直觉似乎不值一提，但正是在这种简单性背后，隐藏着无数有趣而实用的应用。

接下来我们一起来看看这里面的知识。

01 鸽巢原理的本质

鸽巢原理的最简单表达是：如果你有比容器更多的物体，那么必定有某个容器会装超过一个物体。

换句话说，如果你试图把超出容器数量的物体放进这些容器中，总会有一个容器被“过度填充”。

让我们从一个经典的比喻开始。假设你有 10只鸽子，但只有 9 个鸽笼。

如果你把这 10 只鸽子放进这 9 个鸽笼里，根据鸽巢原理，至少有一个鸽笼里会装有两只或更多的鸽子。

这就是鸽巢原理的核心：当物体的数量超过容器时，“重复”或者“冲突”是不可避免的。

10只鸽子放进9个鸽笼，必有一个笼至少两只｜图源 wiki

02 简单例子中的数学魅力

虽然鸽巢原理看起来非常直观，但它在数学中的应用却异常广泛。

鸽巢原理可以帮助我们解决各种实际问题，甚至一些看似非常复杂的问题都可以通过它的简单逻辑来解决。

例子 1：反直觉的生日悖论

设想在一个房间里有 23 个人，那么其中至少有两个人生日相同的概率超过 50%。

特定人数对应的2个人生日一样的概率

这听起来似乎有些反直觉，因为一年有 365 天，23 个人中有两个人在同一天生日的几率看起来应该很小。

但事实上，通过鸽巢原理我们可以理解这个现象。

365 天就好比365个“鸽笼”，而23个人相当于23只鸽子。

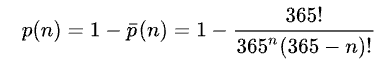
p(n）表示n个人中至少两人同生日的概率

由于物体（人）的数量小于容器（天数）的数量，我们无法立刻得出结论。

但通过进一步的计算可以发现，即使在这个看似较小的范围内，两个或更多人生日相同的概率已经超过了50%，这个现象也得以解释。

感兴趣的朋友可以自己计算。

例子 2：袜子问题

假设你有三种颜色的袜子——红色、蓝色和绿色，每种颜色有两双。

你随机从一堆袜子中抽出四只，问题来了：你抽出的四只袜子中，是否一定有两只是同样颜色的？

根据鸽巢原理，答案是肯定的。

这里的袜子颜色相当于容器，而袜子本身是物体。由于你有三种颜色，而抽出的袜子有四只，鸽巢原理告诉我们：必然有两只袜子颜色相同。

这是鸽巢原理在组合数学中的一个简单应用。

03 数学证明

当然，鸽巢原理也有自己的数学证明方法

鸽巢原理的证明其实非常简单。我们可以通过反证法来进行推导：

1. 假设n > m且每个容器中最多只能包含一个物体。

2. 那么，我们最多可以将 m 个物体放入 m 个容器中，每个容器刚好放一个物体。

3. 然而，这样做后，剩下的 n - m  个物体将无法被放入任何容器中，这显然矛盾。

4. 因此，至少有一个容器中必须包含两个或更多的物体。

这个简单的证明方法展示了鸽巢原理的逻辑力量，尽管它看起来非常直观，但却能够有效地解决很多复杂的数学问题。

05 鸽巢原理的应用

鸽巢原理不仅在数学证明中有广泛的应用，还在现实生活中的许多问题中发挥着作用。以下是一些鸽巢原理应用的具体场景：

1️⃣ 计算机科学中的应用

在计算机科学中，鸽巢原理被用来分析算法效率和存储空间。

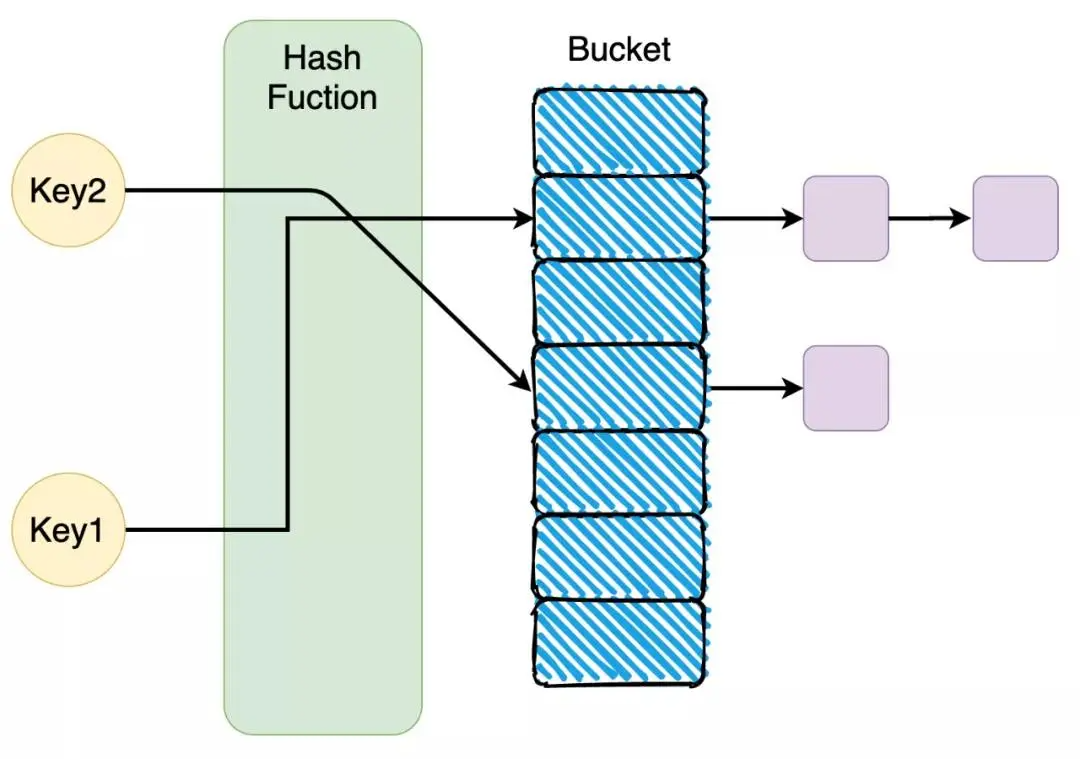
例如，在哈希表中，鸽巢原理可以帮助解释哈希冲突的产生。如果你有更多的键值对（物体）需要存入哈希表（容器）中，而哈希表的槽位数不足，则会不可避免地出现哈希冲突，即多个键值对会被映射到同一个槽中。

设想一个电商平台的用户管理系统，使用哈希表来存储用户信息。系统中的每个用户都有一个唯一的用户 ID，通过哈希函数将用户 ID 转换为哈希值，并映射到哈希表的某个位置。

假设系统当前有 1,000,000 个用户，而哈希表的初始大小是 100,000 个槽位（即哈希表有 100,000 个位置来存储这些用户数据）。这意味着哈希表中有 100,000 个容器，而有 1,000,000 个用户需要放入这些容器中。

根据鸽巢原理，由于用户数量（1,000,000）远远大于槽位数量（100,000），至少有一个槽位会存储不止一个用户的信息。这就意味着哈希冲突是不可避免的，且随着用户数量的增加，冲突的发生频率也会增加。

为了应对哈希冲突，计算机科学家们提出了多种解决冲突的方法：

链地址法（Chaining）：在链地址法中，每个哈希槽都包含一个链表。当多个用户的哈希值被映射到同一个槽时，它们会被存储在该槽位的链表中。这样，虽然槽位相同，但可以通过遍历链表找到相应的用户信息。

鸽巢原理解释了为什么会出现这种情况——因为用户数大于槽位数，必定会有多个用户被分配到相同的槽位，因此链表的使用是不可避免的。

开放地址法（Open Addressing）：在开放地址法中，当发生冲突时，系统会通过某种策略（如线性探测、二次探测或双重哈希）在哈希表中寻找下一个空闲槽位来存储冲突的用户数据。

这种方法避免了链表的使用，但当表中有大量用户时，解决冲突的时间复杂度会增加。

2️⃣ 通信中的应用

在通信网络中，鸽巢原理被用来分析带宽分配的问题。

如果网络中的用户数量超过了可用的带宽通道数量，那么至少有一个通道会被多个用户同时使用，这会导致网络拥塞或传输延迟。

假设在一个拥挤的公寓楼里，有 15 个 Wi-Fi 路由器同时在 2.4 GHz 频段上工作。

由于该频段只有 11 个可用信道（相当于11个“鸽巢”），而 Wi-Fi 路由器有 15 个（相当于15只“鸽子”），根据鸽巢原理，必然会有多个路由器共享同一个信道。

这种情况下，信道冲突不可避免，网络性能也会因此下降。

Wi-Fi 路由器共享同一个信道时，会出现所谓的信道干扰，也就是多个设备在相同的频率范围内同时发送数据，这会导致数据传输的效率降低。

由于信道是有限的，而设备数量超过了信道数量，根据鸽巢原理，至少有一些设备会出现信道冲突，导致干扰。

而鸽巢原理在网络优化和容量规划中起到了关键作用，详细的原理我们以后再谈。

3️⃣数论中的应用

在数论中，鸽巢原理帮助证明了一些关于整除性和同余的命题。

例如，鸽巢原理可以用来证明：在任意 n + 1 个整数中，必然有两个整数的差是 n  的倍数。

这是因为根据鸽巢原理，这些整数可以按同余类进行分类，而超出的整数必定会被归到相同的类中。

鸽巢原理虽然看起来非常基础，但它的应用极为广泛，甚至在数学的某些分支中起到了奠基性的作用。

例如，拉姆齐理论（Ramsey Theory）就是基于鸽巢原理的扩展，用来研究如何在混乱中找到某种秩序。

拉姆齐理论告诉我们，无论如何对某些对象进行分类，总会存在某种形式的结构。

例如，假设你有一张足够大的图，其中每个顶点通过边相连，那么在这个图中，必然存在某种规模的子图，其边都具有相同的颜色。这是鸽巢原理的高级应用，通过简单的分类推导出复杂的结构。

总结

看得出很多貌似深奥的科学知识实际都来自于对大自然的体验和观察。

鸽巢原理是一个表面上看似简单，但实际上在数学和现实生活中都有着深远影响的原理。

通过深入理解鸽巢原理，我们不仅能够掌握一种强大的数学工具，还能够更好地应对许多现实中的挑战。