卡尔在研究生时期曾深陷抑郁症的泥沼，甚至一度想要放弃生命。幸运的是，他的妻子劳拉，一位才华横溢的数学天才，如同一束光照亮了他的世界，将他从深渊中拯救出来。
他们的爱情故事始于卡尔最黑暗的时期，劳拉的智慧和光芒不仅治愈了卡尔的心灵，也为他们的生活带来了希望和支撑。23岁时，劳拉完成了震惊全球数学界的博士论文，人们甚至将她誉为当代的冯·诺伊曼。
她对数学的热爱近乎痴迷，如同飞蛾扑火般执着追求着数学的真理。
2.无法承受的真实：1=2然而，在一次深入的研究中，劳拉遭遇了足以撼动她整个学术生涯的难题。她不满足于解决已知的数学问题，雄心勃勃地试图改写现有的公理系统，构建一个全新的数学体系。
在这个过程中，她惊恐地发现，自己建立的体系虽然完美自洽，却导出了一个令人难以置信的结论：1=2。这个结论的恐怖之处在于，它意味着任何数字都可以等于其他数字，数学的基础将不复存在，整个数学大厦都将轰然倒塌。
3.寻找答案与无尽的折磨劳拉被困扰和焦虑所吞噬，她寻求其他顶尖数学家的帮助，希望能够找出自己体系中的错误。然而，所有的检验结果都指向同一个令人绝望的事实：她的体系没有任何逻辑错误。
这意味着，一个完美自洽的数学体系却推翻了数学本身的基础。这使得劳拉的精神状态濒临崩溃，陷入了一种近乎疯狂的状态。
她的丈夫卡尔，虽然尽力通过陪伴和开导来帮助她，却无法理解她所面临的困境的深度和严重性。卡尔将劳拉的发现与非欧几何和虚数系统的出现相类比，认为这些看似悖论的理论最终都能够被解释和解决。但他没有意识到，劳拉的困境远比这要深刻得多，它触及了数学的根基——“除以零”的概念。如果任何数都可以除以零，那么任何两个数字都将相等，整个数学体系将彻底崩溃。
4.数学的牢笼：一致性的追寻早在1900年的国际数学大会上，德国数学家大卫·希尔伯特就提出了23个悬而未决的重大数学问题，其中第二个问题便是证明算术在逻辑上的一致性。数学家们一直致力于证明数学的逻辑一致性，尽管这些看似不证自明的陈述无法用形式化的方法证明。
1931年，库尔特·戈德尔证明了两个震撼人心的定理：第一个定理指出，数学或许是真实的，但我们无法证明它的真实性；第二个定理则指出，算术的逻辑一致性是不可证的。即使在1936年，德国数学家根岑尝试用超限归纳法证明算术一致性，其结果也充满争议，并未被数学界普遍接受。
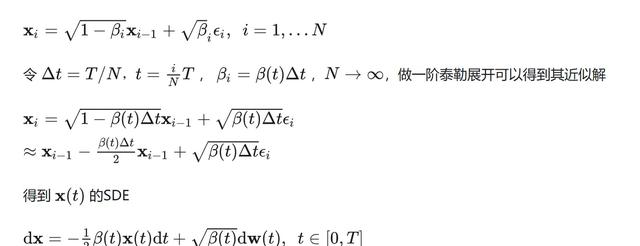
这些理论和发现揭示了理性知识的脆弱性，数学家们深知，他们所信仰的体系始终面临着无法解决的根本性矛盾，而劳拉正是被这种认知所折磨，被困在了数学的牢笼之中。
