Your experience with things that you have seen before is inadequate, is incomplete.The behavior of things on a very tiny scale is simply different.

——Richard Feynman

理查德·费曼强调，我们的日常经验不能完整地描述事物的本质，特别是在微观尺度上。费曼因研究光的量子物理以及其与物质的互动而获得了诺贝尔奖。在他年轻时，作为一个研究生，他首次提出了一种全新的看待量子力学的方式，被称为路径积分公式（Path Integral Formulation）。这个概念对于我们对量子物理的认知起到了核心作用。它不仅为我们提供了关于量子世界反直觉行为的深入理解，还揭示了如何从量子描述中得出经典的物理定律如F=ma。

经典物理学和量子物理学在预测粒子位置方面有着根本的差异。在经典物理中，我们可以通过合并所有的力并使用方程来准确地预测一个粒子在任何特定时间的位置。

例如，一个自由粒子沿直线移动，而一个被投向空中的棒球将沿着抛物线轨迹。相对地，在量子力学中，我们只能预测粒子在某个位置被发现的概率。这意味着即使多次重复同一实验，粒子的位置也可能每次都不同。这种概率性特质是量子物理中最令人震惊的特点之一，它指出量子粒子不再沿着单一确定的路径从一点移动到另一点。

实际上会考虑所有可能的路径，并将这些可能性进行累加。这种累加所有可能路径的方法被称为费曼路径积分，它是一个非常出人意料的概念。一个经典物体，如棒球，是如何遵循一个明确路径的，同时又与量子的总路径累加理念相协调，是物理学中最深奥的主题之一。

我们想要知道一个量子粒子从开始时间t_i的位置x_i移动到后续时间t_f的位置x_f的概率。在量子力学中，这种概率是由振幅得到的，这是一个复数。通过计算振幅的绝对值的平方，就得到了实际的概率。

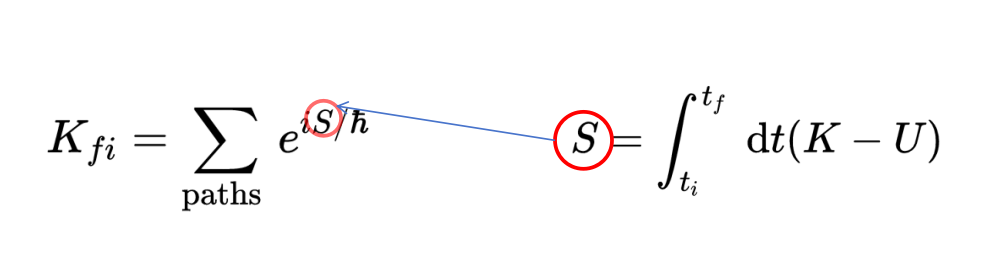
为了确定粒子从点i到点f的振幅（记为K_fi），费曼提出了路径积分的概念。与经典物理中粒子沿着单一轨迹移动的观点不同，费曼在量子力学中提出，我们应该考虑所有可能的路径。每条可能的路径都有一个特定的权重，由下面的表达式表示，

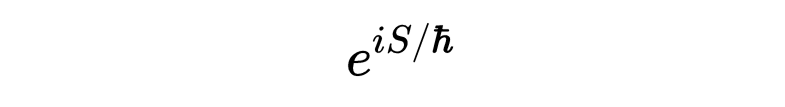
其中，ℏ是量子力学中的基本常数——普朗克常数，而S代表与每条路径相关的作用量。

作用量是经典力学方法中的核心对象，被称为拉格朗日公式（Lagrandian Formulation）。为了计算一个量子粒子从点i移动到点f的总振幅，费曼提出将所有可能的路径贡献加总。

这不仅仅是简单的累加，而是涉及一种称为“路径积分”的复杂积分方法，这也是它被称为量子力学的路径积分公式的原因。我们经常用这个公式表示它

费曼的这个理论基于双缝实验（Double-slit experiment），因此双缝实验为我们提供了理解这一复杂概念的基础。

双缝实验

双缝实验是物理学中的一个经典实验，旨在探索光和物质的波动性和粒子性。以下是该实验的简要描述。

实验设置：在一个屏障上制作两个相距非常近的小缝，这个屏幕后面再放一个检测屏或者传统的胶片来记录通过缝隙后的波或粒子分布。

经典粒子的结果：当向这两个缝投射经典粒子（如小球）时，检测屏上会出现与每个缝对应的两个分布区域。简单来说，每个粒子都会通过其中一个缝，并在其后的区域撞击。

波的结果：当用波（如光波）照射两个缝时，从两个缝出来的波会相互干涉。在检测屏上，会出现交替的明亮和暗区，这被称为干涉图案。明亮的区域表示波的峰值和谷值相加，形成构造性干涉；暗的区域表示一个波的峰值与另一个波的谷值相遇，它们相互抵消，形成破坏性干涉。

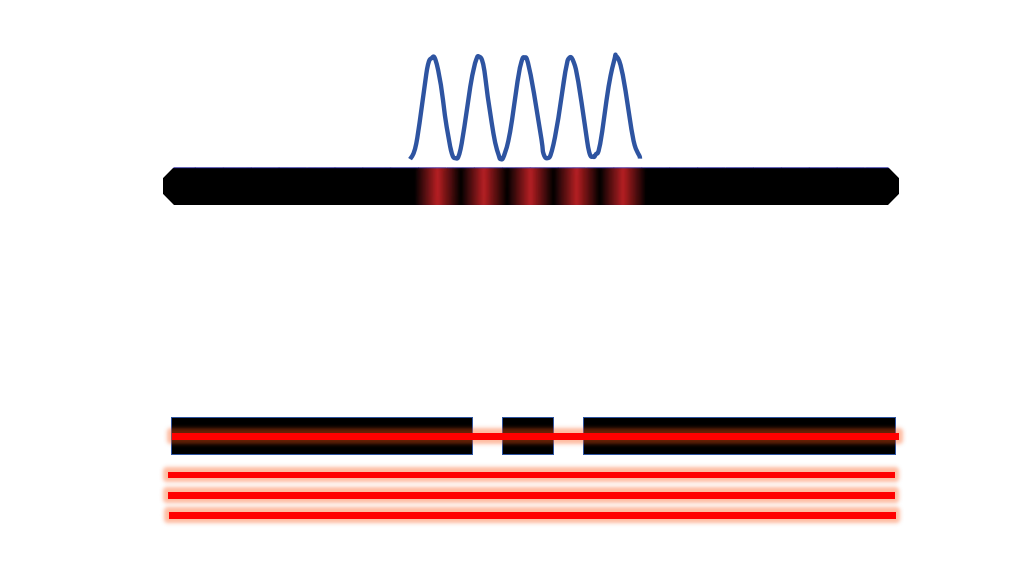
量子粒子的结果：当使用量子粒子（如电子）进行实验时，结果变得更为有趣和神秘。当一次只发射一个电子时，我们预期会看到与经典粒子类似的两个分布。但实际上，电子在检测屏上形成了与波类似的干涉图案。这意味着单个电子似乎同时“感知”了两个缝，就好像它经历了所有可能的路径。

费曼的路径积分方法为我们提供了一个全新的视角，帮助我们理解量子现象。与薛定谔的波函数方法不同，费曼的方法没有试图描述一个粒子在特定时间的状态，而是强调了从起始到结束状态的所有可能路径的重要性。

当在屏障上增加第三、第四、第五个孔时，我们不仅需要考虑穿过每一个孔的路径，还需要考虑这些路径之间的所有可能组合。

当我们引入更多的屏障和更多的孔时，要考虑的路径组合变得越来越复杂。

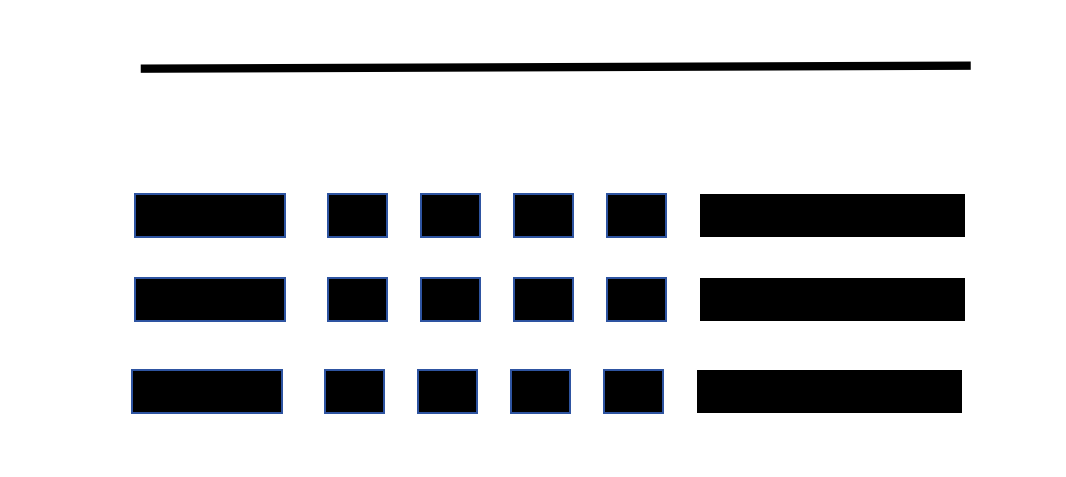
极端情况下，如果我们连续增加孔并使屏障靠得足够近，它们实际上会消失，留下一个没有任何物理障碍的开放空间。

所有可能的轨迹：在没有障碍的空间中，为了计算从起始点到终点的总振幅，我们需要对所有可能的路径中的每一个路径产生的振幅进行总和。

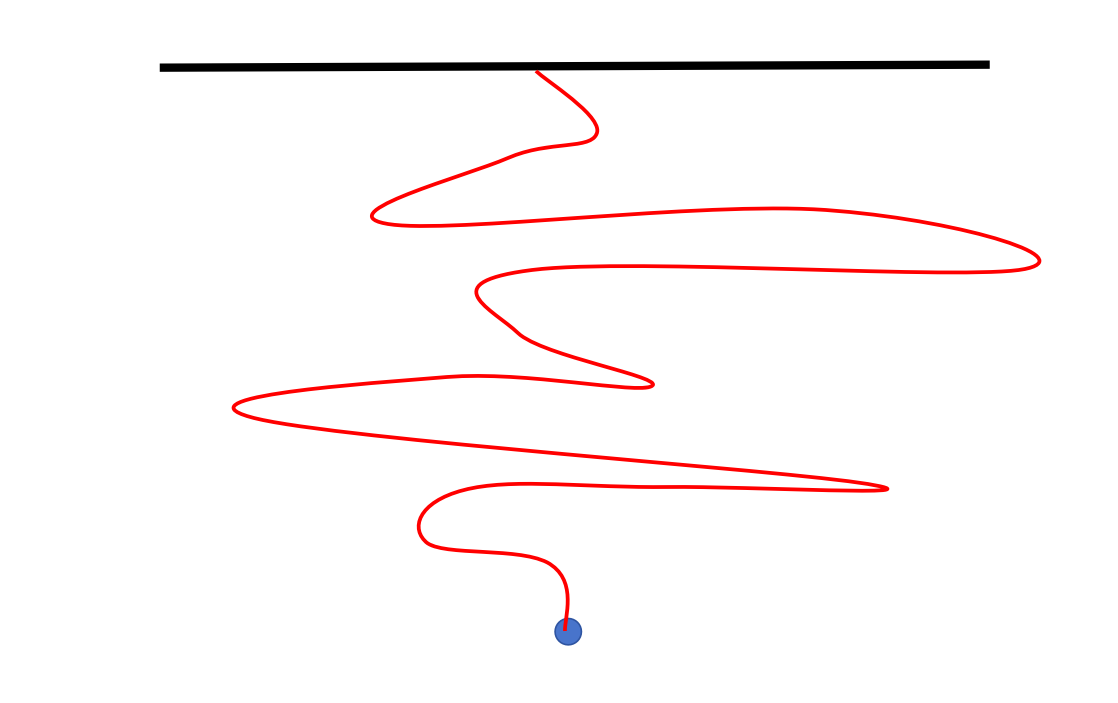
这些可能的轨迹不仅限于空间，而且还包括时间。这意味着一个粒子可以采取各种各样的时间轨迹，从早到晚，或甚至可能从晚到早（虽然这在我们的日常经验中是不可能的）。

为了确定从起点到终点的粒子的总的可能性或振幅，我们必须考虑所有这些可能的路径和时间轨迹，并为每一个都赋予一个特定的权重。但问题是，我们应该为每个路径分配什么权重？

为此，每个路径都被赋予一个特定的复相位

其中Φ是我们为每条路径分配的某个数字，它决定了它如何为总振幅做出贡献。这意味着每条路径对总振幅的贡献都是以一个具有确定相位的单位复数的形式出现的。在复平面上，这可以表示为一个长度为1、角度为Φ的箭头。

核心的问题是如何确定每个路径的相位Φ。答案与路径的物理属性有关，具体来说，与所谓的“作用量（action）”S有关。每条路径的复相位由

给出，其中ħ是普朗克常数。作用量在经典物理中是一个核心的概念，定义是：粒子的动能与其势能之差在某段时间内的积分，

具体来说，作用量是从时间t_i到t_f的动能K与势能U之差的积分。这个被积分的量，K-U，被称为拉格朗日量（Lagrangian），它是经典力学中的一个关键概念，尤其在所谓的拉格朗日力学中。

下面解释这个权重的由来，

首先，普朗克常数ħ是量子力学的关键常数，具有能量和时间的单位。

由于Φ是无量纲的角度（以弧度为单位），因此必须有某种方式消除这些单位。作用量S和ħ的比值提供了这种消除机制，确保了e^(iS/ħ)这个表达式在单位上的正确性。

此外，动能K和势能U是能量单位，与时间相乘时会得到作用量S的单位。尽管可能认为使用动能和势能的总和更为直观，但实际上应该取它们的差值。这个选择背后的原因将在后续的讨论中进一步解释。

如何从量子力学中得出F=ma？

当我们将观察的尺度从微观的量子粒子扩展到宏观的日常物体时，经典的物体轨迹会变得明显。费曼提出的方程初看起来有些反直觉，因为它似乎建议我们对一个粒子可能走的所有路径求和，而每条路径仅仅在相位上有所不同。那么如何解释在我们日常生活中明确看到的现象，例如一个棒球沿一个清晰的抛物线路径飞行？

这是量子力学和经典力学的交集问题。既然量子力学是一个更为基础的理论，我们的日常经典规律必须能够从它中得出。费曼的路径积分方法提供了一个最深入的见解，解释了为什么这种从量子描述到经典描述的过渡是可能的。简而言之，对于大型物体，例如棒球，路径积分中的大多数项在求和时会相互抵消，留下的只是那条经典轨迹。

原因是这样的，当我们试图了解为何大多数路径在费曼的方法中会互相抵消时，我们可以考虑每一条路径如何在复平面上被表示。

每个路径都可以被想象为复平面上的一个单位长度的箭头，其角度由路径的作用量S除以普朗克常数ħ确定。每当我们选取一条特定的路径，我们就会根据它的作用量计算出这个角度，并在复平面上描绘出相应的箭头。

但是，普朗克常数ħ的值非常非常小，大约是10^-34，这意味着任何微小的作用量变化都会导致在复平面上的巨大角度变化。因此，即使两条轨迹只有细微的差异，它们在复平面上的箭头可能会指向完全不同的方向。

考虑到这一点，当我们考虑所有可能的轨迹时，会得到一系列指向各种随机方向的箭头。根据费曼的路径积分方法，我们需要将所有这些箭头合并。但因为它们指向各种不同的方向，所以当我们把它们全部加在一起时，它们几乎会相互抵消，仿佛什么也没有得到。

这就解释了为什么，在考虑所有可能路径的时候，只有那些经典的路径不会被其他路径抵消，从而在宏观尺度上得到显著的效果。

对于宏观尺度的经典物体，由于其作用量S远大于普朗克常数ħ，路径积分中的大多数项都会相互抵消，只留下少数项。关键是要找到那些作用不会因为轻微的轨迹变化而产生大的变化的路径。这些路径及其附近的路径的作用量都大致相同，所以它们在复平面上表示的箭头方向都相似，这些箭头就不会相互抵消。

设想有这样一个特别的路径，即使你对其进行轻微的调整，它的作用也几乎保持不变。这些路径及其附近的路径在求和时会相互加强，而其他的路径则会相互抵消。这种具有相似作用和不会因微小变化而改变其作用的路径被称为“静态路径（Stationary path）”。

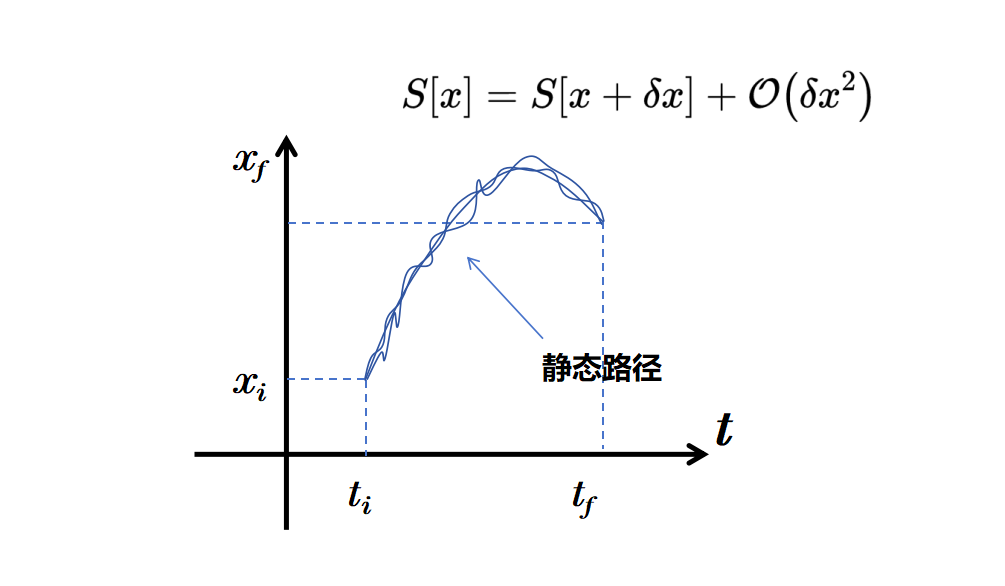
静态路径在求和中的主导作用可以这样理解：考虑一个静态路径，并对其引入一些微小的扰动，这个新的路径的作用与原路径相似，至少在第一近似中是这样。

这和我们找到函数的平稳点（例如最小值点）的想法是一样的：在这样的点上，函数值不会因为沿函数移动一小段距离而发生显著的变化，因为在这些点上的斜率为零。

寻找静态路径与寻找函数的稳定点相似，只是现在我们正在探索的是一个连续的轨迹，而不仅仅是一个点。不过，在经典物理的边界下，主导路径积分的实际上只有静态作用的路径。令人惊讶的是，这些静态路径其实就是我们所称的经典路径。

总的来说，当你将作用量的数学表达式代入静态条件时，

会发现满足方程

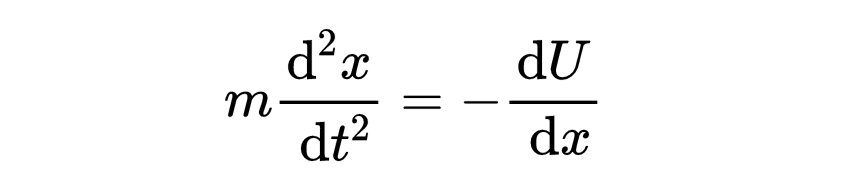
的轨迹是静态的。这实际上就是经典力学中的F=ma，这里的力与势能的关系为力等于势的负导数。

而路径积分得出F=ma 的原因并不是因为经典路径给出了一个巨大的贡献，从而占了上风。事实上，每个路径对总和的贡献都是1。经典路径能够胜出的原因在于，其对应的作用是静态的，这意味着所有靠近该路径的箭头在复平面上都朝着相同的方向，从而它们叠加起来而不是相互抵消。但这只是对于像棒球这样的宏观物体来说。对于像电子这样的小粒子，其作用量接近于普朗克常数，因此，与普朗克常数的比不再是一个巨大的数值，这也意味着在量子尺度上，不仅仅是经典路径可以给出有效的贡献。实际上，可能有许多不同的路径都对量子粒子的行为产生影响，这使得经典的F=ma 在这里不再那么至关重要。

我之前提到过，如果我们在定义作用量时选择一个不同的符号，即用K+U而不是K-U，那么静态路径的方程仍然是有效的，但是U的符号会变成相反的。这将导致得出ma=−F 而不是经典的F=ma。因此，为了正确地重现经典物理的预测，我们确实需要使用K−U。

当一个经典粒子的轨迹使作用量最小化时，这个现象被称为“静态作用量原理”或“最小作用量原理（Principle of Least Action）”。在许多情况下，经典轨迹确实是作用量的最小值，所以“最小作用量原理”这个名字更为普遍。这一原理是经典物理学的基石，实际上比F=ma更为基础。