“a”的值是多少？答案在于你能否根据“a”找到三角形的底边

您认为“a”的值是多少？

这个问题的答案在于你能否根据“a”找到三角形的底边。

你会怎么做？

提示：根据“a”求出三角形的底边。

这个三角形是等边三角形。

根据“a”求出三角形底边只是解决方案的一部分。我们还需要将其与三角形边的已知值相等，以得出“a”的值。

然而，没有给出三角形的边。

这表明问题并不完整。只有少数人注意到了这一点并做出了适当的假设。我赞扬你的努力！

完整的问题如下：

这告诉我们，由于它是等边三角形，因此它的每一边都是 1。

让我们首先标记形状上的几个点。

从该图中，我们知道了“a”这个基数的很大一部分，但是我们对 CD 和 FG 的长度一无所知。

三角形BCD与三角形EFG相似。

令 CD 为x。由于所涉及的三角形相似，因此 FG 为3x

三角形的底边变成

x + a + 2a + 3a + 3x = 6a + 4x

现在，我们来考虑三角形 bcd。记住，角 bcd 为 60 度（因为较大的三角形是等边三角形）。

这让我们更清楚地看到三角形 bcd。

目标是找到x。

我们能在a和x之间建立关系吗？当然可以！

记住三角函数。

这意味着：

Tan60 度是 3 的平方根。

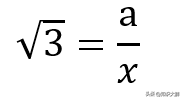
好了！x = a/sqrt(3)

记住，三角形的底边是6a + 4x

6a + 4x = 1

从这里，我们可以用x的值代替以a 为底数。

这给了我们：

让我们合理化

分解“a”，我们得到：

现在，让我们对分母进行有理化，

通过简化，我们得到：

好了！我们找到了a的值！