潜入数学的深渊，你会发现一片无垠的领域，犹如一座无边无际的森林，其中的每一棵树，每一片叶子，都饱含了生机与奥秘。在这座森林中，有一片神秘的区域被我们称为"函数空间"。

当我们处理实数或复数时，一个数x有一个自然的大小概念，即它的模|x|。我们也可以利用这一个大小的概念来定义两个数x和y的距离

由此可以说，哪些成对的数是互相接近的，哪些是远离的。

然而，当处理具有较多自由度的对象时，情况就变得比较复杂。举例来说，考虑决定一个3维矩形箱子的“大小”，这里有好几个量可供选用：长、宽、高、体积、表面积、直径（最长的对角线长度）、扁平率等等。不幸的是，用这些量作出的大小比较并不是等价的。例如，箱子A可能比箱子B长一些，而且体积也比较大，但是箱子B可能宽一些，而且表面积大一些。由于这个原因，人们放弃了箱子应该只用一个量来表示其大小的想法，而接受了另一个思想：有许多这样的大小概念，它们都可能是有用的，在有些应用里，把大体积的箱子和小体积的箱子分开来；在有些应用里，可能想把扁平的箱子和圆一点的箱子分开来。当然，不同的大小概念有一些关系（例如等周不等式）。它们在已知表面积时，对体积的可能值给出了一个上界，所以，情况并不像初看起来那样漫无头绪。

现在回到具有固定的定义域和值域的函数，

（最好心里记住一个定义在区间[-1，1]上而值在实直线R中的函数f：[-1，1]→R，这是一个好的例子）。

这些对象有无穷多自由度，所以毫不奇怪，这里也有无穷多不同的“大小”概念，而它们都对于“一个已给的函数有多大"这个问题（或者对一个密切相关的问题：“两个函数f和g有多么接近?"）提供了不同的答案。有时候，一些函数在某种度量下有无穷的大小，而在另一种度量下则只有有限大小（类似地，一对函数可能在某种度量下非常接近，而在另一种度量下距离很远）。这里的情况又可能看起来很混乱，但是它仅是反映了一个事实，即函数可能有许多不同的特性——有的高，有的胖，有的光滑，有的震荡，等等，而按照不同的应用，可能更着重于一种特性，而不是另一种。在分析里，这些特性都体现在种种标准的函数空间及其相关的范数上，而这些范数，既可定量也可定性地描述这些函数。

形式地看，一个函数空间常是一个赋范空间X，其元素是一些函数（具有固定的定义域和值域）。在分析中考虑的标准的函数空间绝大多数（但肯定不是全部）不仅是赋范空间，还是巴拿赫空间。X中的函数f的范数：

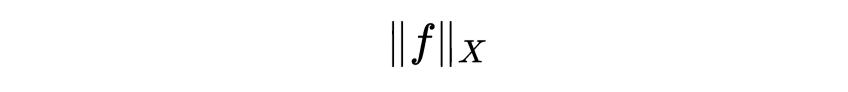
就是这个函数空间量度这个函数f有多大的方法。

巴拿赫空间是完备的赋范向量空间，也就是说，它是一个在某种范数下的向量空间，并且这个空间是完备的。完备性是指对于空间中的任何柯西序列（Cauchy sequence），它在该空间中都有极限。

通常（但非一定如此）范数是由简单的公式给出的，而空间X就是由那些使得

有意义并且为有限的函数构成的。这样，仅就函数f属于函数空间X这一事实，就已经传递了关于这个函数的定量的信息了，例如，它可能包含了f正规到何种程度，它衰减多么快，它以什么常数为界，或者它的积分有多大，等等。

现在给出一些常用的函数空间的样本。为简单起见，仅限于考虑由[-1，1]到R的函数的空间。

这个空间由所有由[-1，1]到R的连续函数构成，通常记作C[-1，1]。连续函数已经足够正规，足以避免那些很粗糙的函数所产生的许多技术上微妙的地方。紧区间（如[-1，1]）上的连续函数是有界的，所以可以加于这个空间的最自然的范数是上确界范数，即|f|的最大值，记作

形式上说，它的定义是

但是对于连续函数，说最大值或者说上确界，是一致的。

上确界范数是与一致收敛性相联系的范数：一个序列f1，f2，…一致收敛于f，当且仅当

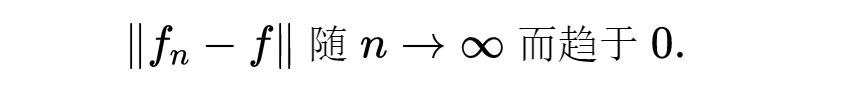
空间C⁰[-1，1]有一个有用的性质，即其中的元素不但可以相加，而且可以相乘，这就使C⁰[-1，1]成为巴拿赫代数的最基本的例子。

另一个函数空间的例子是：

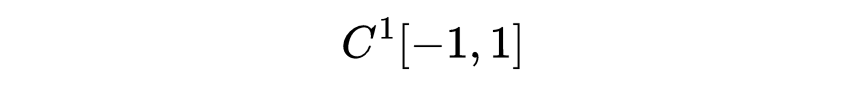
这是一个对成员的资格限制比C⁰[-1，1]更严的空间：C¹[-1，1]中的函数f不仅是连续的，而且它的导数在[-1，1]上也是连续的。上确界范数现在不是一个自然的范数，因为一个连续可微函数序列可以在C⁰[-1，1]范数下收敛于一个不可微的函数。现在应该定义

注意C¹范数现在不仅量度函数本身的大小，还量度了其导数的大小（但是仅仅管住导数也不能令人满意，因为那会给常值函数以零范数）。因此这是一个保证了比上确界范数更高的正规性的范数。可以类似地定义二次连续可微的函数的空间

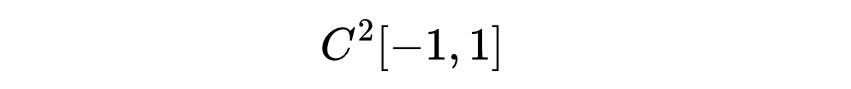
等等，一直到无穷可微函数的空间

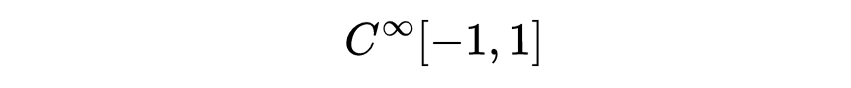
但是最后这个空间并不是赋范空间（这些空间还有“分数阶”的版本，例如

即满足α阶赫尔德（Otto Ludwig Holder，德国数学家）条件的函数的空间。

第三个函数空间的例子：勒贝格空间

上面给出的上确界范数

对于所有的x∈[-1，1]管住了|f（x）|的大小。然而，这意味着如果有x的一个很小的集合，使得|f（x）|在其上很大，则

哪怕对于典型的x，|f（x）|会小得很多。有时，取一个不那么受函数在小的集合上的值影响的范数会更加有利。函数f的LP范数是

当1≤p<∞时，它对于（使得上面的积分有限的）可测函数有意义。这些函数构成

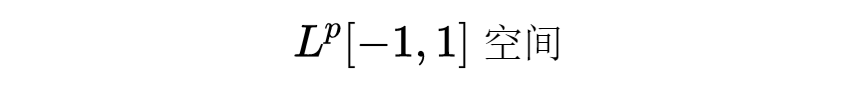
可测函数f的范数

是它的本质上确界，这个概念粗略地说，就是在函数的定义域中略去了一个测度为0的集合，然后求此函数在此零测度集合的余集合上的上确界，最后再求这些上确界的下确界。那些使得

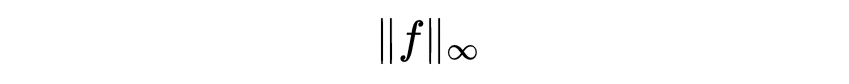
保持有限的函数构成一个函数空间，记作

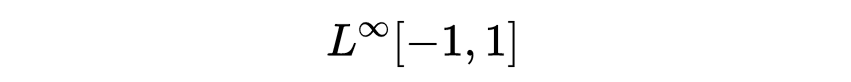
如果此函数是连续的，则在定义域中略去一个0测度集合，不会影响其上确界，所以

与

可以证明，当p→x时，

可以说，

范数量度的是函数的“高度”，

而

L^P范数量度的是函数的“高度”和“宽度”的综合。

这些范数中，特别重要的是L²范数，因为L²[-1，1]是一个希尔伯特空间。这个空间有特别丰富的对称性：存在非常丰富的种种酉变换，即定义在

最后一个函数空间的例子：索伯列夫空间

勒贝格范数在一定程度上控制了函数的高度和宽度，但是对于函数的正规性未置一词；一个L函数没有理由是可微的，甚至没有理由是连续的。为了把这些信息也放进来，我们要转到索伯列夫（Sergei Lvovich Sobolev，前苏联数学家）范数

其定义是

索伯列夫空间就是使得这种范数为有限的函数所成的空间。这样，一个函数在索伯列夫空间中当且仅当它和它的直到k阶的导数都在

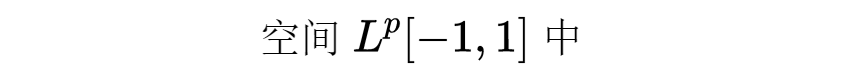
这里有一点细微之处：我们并不要求f在通常意义下k次可微，而是在较弱的分布的意义下k次可微。例如，函数f（x）=|x|在零点并不可微，但是它确有一个自然的弱导数：

这个函数属于

（因为集合{0}的测度为0，所以不必指定f'(0)之值。所以f属于

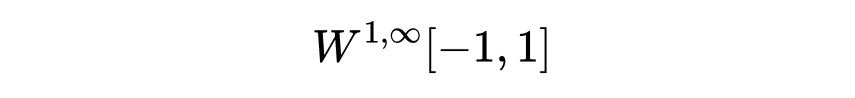
这个空间就是利普希茨连续函数所成的空间。我们需要考虑这些广义可微的函数，因为否则

在对偏微分方程和数学物理作分析研究时，索伯列夫范数特别有用。例如

范数可以解释为与此函数相联系的“能量”（的平方根）。

函数空间的构造在许多方面有助于研究函数。例如，如果在函数空间中有了一个好的基底，使得此空间的每一个函数都可以写成这个基底的（可能是无穷的）线性组合，而且对于这个线性组合如何收敛于原来的函数有一些定量的估计，这就使我们能有效地用一些系数来表示这个函数，而且可以用更光滑的函数来逼近它。例如，关于

的一个基本的结果是，普兰舍利定理指出，除了其他结果外，还有：存在复常数序列

使得当N→∞时，

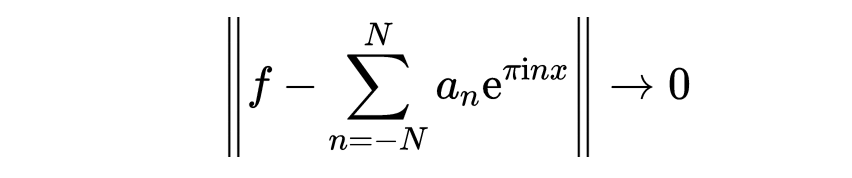
这个结果表明，L²[-1，1]中的任意函数都可以在L^2中用三角多项式，即形如

的表达式，逼近到任意精确度，这个复数序列中的an就是f的第n个傅里叶系数，它们可以用下面的公式来表示：

可以认为，这个结果说的就是函数序列

（实际上，它们构成规范正交基底，即每个元素的范数均为1，而且任意两个不同元素的内积都是零）。

关于函数空间的另一个很基本的事实是，有些函数空间可以嵌入其他函数空间，所以这个空间的所有函数自动地也属于另一个空间。进而，时常存在一个不等式，用另一函数空间的范数来给出此函数空间范数的上界。例如，一个高正规性空间如C¹[-1，1]的函数自动地属于一低正规性空间如C⁰[-1，1]，而一个高可积性空间如中的函数自动地属于一个低可积性空间。这些包含关系不能反转过来。然而，确实有所谓索伯列夫嵌入定理，使我们能以正规性“交换”可积性。这种结果告诉我们，具有很多正规性但是可积性不足的空间，可以嵌入到具有低正规性但是高可积性的空间里面。下面这种估计

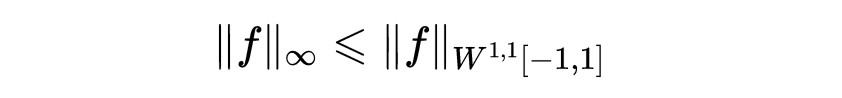
就是这种定理的一个样本。它告诉我们，如果|f(x)|和|f'(x)|的积分都有限，则函数f必定是有界的。

再一个非常有用的概念是对偶性的概念。给定一个空间X，就可以定义其对偶空间X*为X上的所有连续线性泛函的空间，或者更精确地说，就是所有的映射

的空间，不过要求它们是线性的，而且对于X的范数是连续的。例如，当1<p<∞ 时，可以证明实的L^P[-1，1]空间上的每一个线性泛函都可以用一个L^q[-1，1]的函数g写为

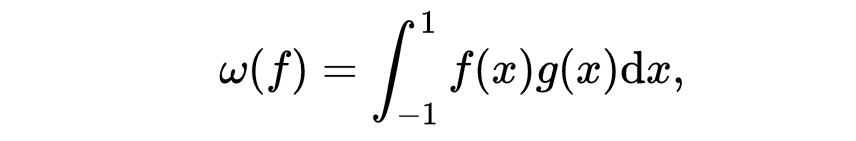
这里的q由等式1/p+1/q=1决定，称为p的共轭指数。

要研究某函数空间的一个函数，有时可以看对偶空间中的连续线性泛函如何作用于这些函数来进行。类似于此，要研究一个从一个函数空间X到另一个函数空间Y的连续线性算子T：X→Y，有时也可以先考虑伴算子T*：Y*→X*来进行。

关于函数空间，我们还要提一个重要的事实，某个函数空间X可以“插入”另外两个函数空间X0和X1中间。例如空间L^P[-1，1]，1<p< 以一种很自然的意义插入

插入的精确定义过于技术化，所以本文不作解释，但是关于它的所谓“插值定理"之所以很有用，是因为有这样一个事实：“极端”的空间X0和X1时常比“夹在中间的”空间更容易研究。例如，可以用它来给出杨（William Henry Young）的不等式以一个初等证明。这个不等式就是说，令1≤p，q，r≤ 满足关系式1/p+1/q=1+1/r，而f，g分别属于

令

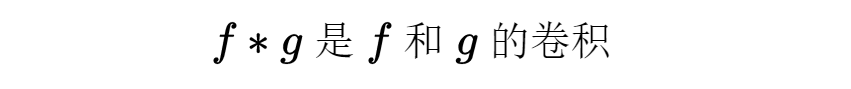
即有

这时，

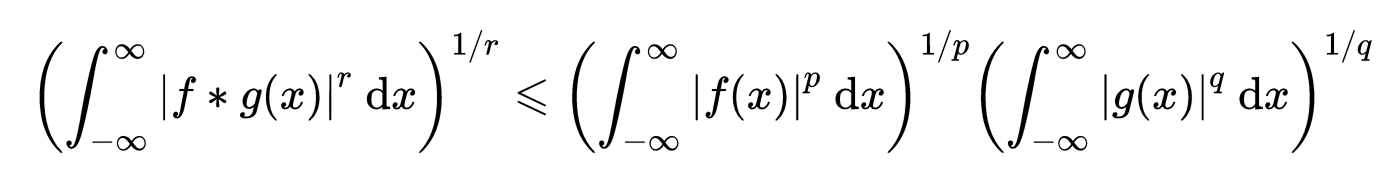
插值定理在这里是很有用的，因为在p=1，q=1或r=x这些极端的情况下，这个不等式很容易证明。如果不借助于插值定理，这个证明就难多了。