行测题库｜数量关系｜每日一练：数学运算54

例题1

甲、乙两工厂共同完成某个生产订单需要12天。现两工厂共同生产8天后，再由乙单独生产7天，完成了订单总量的90%。问若整个订单是乙单独生产，需多少天完成？

A.20

B.23

C.26

D.30

解析：

设甲的效率为x，乙的效率为y。

根据题意可列方程：12×90%（x+y）=8（x+y）+7y，整理可得x∶y=3∶2。

赋值甲的效率为3，乙的效率为2。

则订单总量为12×（3+2）=60。

若整个订单是乙单独生产，需60÷2=30天。

知识点：

工作总量=工作效率×工作时间。

工作时间=工作总量÷工作效率。

例题2

为发展乡村旅游，某地需建设一条游览线路，甲工程队施工，工期为60天，费用为144万元；若由乙工程队施工，工期为40天，费用为158万元。为在旅游旺季到来前完工，工期不能超过30天，为此需要甲、乙两工程队合作施工，则完成此项工程的费用最少是：

A.156万元

B.154万元

C.151万元

D.149万元

解析：

根据“甲工程队工期为60天”，“乙工程工期为40天”，可赋值工程总量为120。

则甲的效率为120÷60=2，乙的效率为120÷40=3。

根据“甲工程队工期为60天，费用为144万元”，可知：甲每天费用为144÷60＝2.4万元。

根据“乙工程队工期为40天，费用为158万元”，可知：乙每天费用为158÷40＝3.95万元。

甲完成1的工作量费用为2.4÷2=1.2万元，乙完成1的工作量费用为3.95÷3≈1.32万元。

要想费用尽可能少，应尽量多用甲。

甲工作30天完成30×2＝60的工作量，剩余120-60=60由乙完成，需要60÷3＝20天。

总费用为2.4×30＋3.95×20＝151（万元）。

因此，选择C选项。

例题3

小王在商店消费了90元，口袋里只有1张50元、4张20元、8张10元的钞票，他共有几种付款方式，可以使店家不用找零钱？

A.5

B.6

C.7

D.8

解析：

枚举如下：

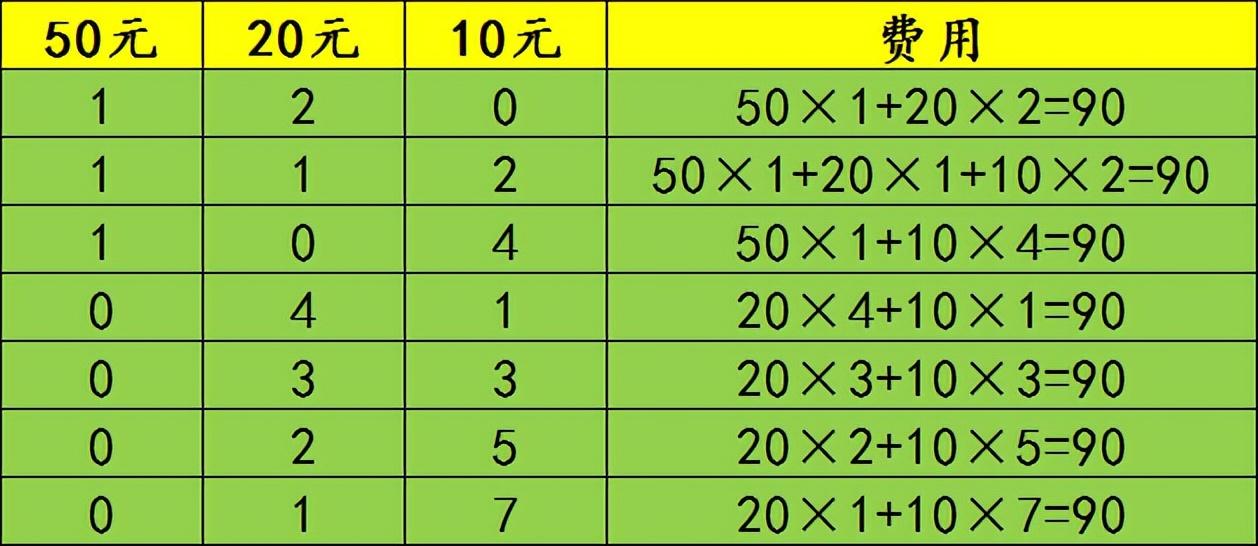
可得，共有7种付款方式，可以使店家不用找零。

因此，选择C选项。

例题4

某品牌网店为迎接“双11”推出优惠如下：满399元减20元，满599元减50元，满999元减100元。甲选购的4件衣服价格分别为：597元、408元、309元、189元。为了享受最大的优惠，最多能减（）元。

A.170

B.150

C.120

D.70

解析：

由于买的越多优惠越多。

597元的衣服和408元的衣服一起购买，可以享受满999元减100元的优惠；

309元的衣服和189元的衣服一起购买，可以享受满399元减20元的优惠。

为了享受最大的优惠，最多能减100＋20＝120（元）。

因此，选择C选项。

例题5

某电子元件制造厂有甲、乙、丙三个车间，甲、乙、丙三个车间的产量分别占总产量的5%、70%、25%，且甲、乙、丙三个车间的次品率依次为4%、3%、2%。任取一件产品，取到次品为乙车间制造的概率是：

A.15%

B.45%

C.75%

D.85%

解析：

赋值三个车间总产量为100个。

根据“甲、乙、丙三个车间的产量分别占总产量的5%、70%、25%”，可知：甲、乙、丙车间产量分别为5个、70个、25个。

根据“甲、乙、丙三个车间的次品率依次为4%、3%、2%”，可知：次品总量为5×4%+70×3%+25×2%=2.8个。

乙车间生产的次品量为70×3%=2.1个。

则取到次品为乙车间制造的概率为2.1÷2.8=75%。

因此，选择C选项。