□唐慧彬
试一试,在下面算式的( )里填上合适的数,使等式成立。

把分数拆分为三个单位分数之和
如果一个数一个数地试算,也能找出正确答案,但费时费力。有没有更简便的方法呢?
由于三个加数的分子都是1,这三个加数都是最简分数,因此把30分之19分成三个分数时,分成的三个分数要么是最简分数,要么是可以约分成分子是1的分数。怎样分才符合这个要求呢?其实只要分成的三个分数的分子都是分母30的因数就行了,30的因数有:1、2、3、5、6、10、15和30。
可是一下子要把30分之19分成三个分数比较困难。可以先确定第一个加数,也就是确定最小的那个加数,然后确定剩下的两个加数。
如果第一个加数是30分之1,另两个加数的和就是30分之18,可以把30分之18分成30分之3+30分之15。把这两个加数约分后得到:30分之1+10分之1+½=30分之19。

如果第一个加数是30分之2,另两个加数的和就是30分之17,可以把30分之17分成30分之2加30分之15。把这三个加数约分后得到:15分之1+15分之1+½=30分之19。

如果第一个加数是30分之3,另两个加数的和就是30分之16,可以把30分之16分成30分之6+30分之10。
把这三个加数约分后得到:
10分之1+5分之1+⅓=30分之19。

经过试算可以发现,再没有符合要求的其他填法了,所以这道题一共有三种填法:

(作者单位:江苏省海安县角斜镇中心小学)
一个单位分数拆分问题的解法探讨编辑同志:
您好!
我是江苏省泰州市教师进修学校的乐家骏,是贵刊的读者,最近在阅读了贵刊(5-6年级)2012年第5期《根据因数思考》一文后,有些看法。首先我们回顾一下原题:
试一试,在下面算式的()里填上合适的数,使等式成立。

问题图
唐老师在文中提出的解题途径是:找出30的所有因数,把19分成三个因数的和,以这三个因数做分子,30做分母,通过约分,就可以找到一种填法。还提出先确定最小的一个加数,再找到其他两个加数。文中列出了三种填法,并认为没有其他填法了。
用以上方法可以找到解决文中问题的一些填法,但不能找到所有的填法,我有另一种解法:先寻找最大的一个加数(因为最大加数的可能值是有限的),然后求出30分之19与最大加数之差,把问题转化为将一个分数分拆成两个单位分数之和的问题。
设

最大的加数a分之1应小于30分之19,但又不小于

即,

则 a 可能是2、3和4。
(1)当a分之1=½时,较大的加数b分之1应小于15分之2,又不小于(15分之2÷2=1/15)15分之1,即

b 可能是8、9、10、11、12、13、14和15。试算:
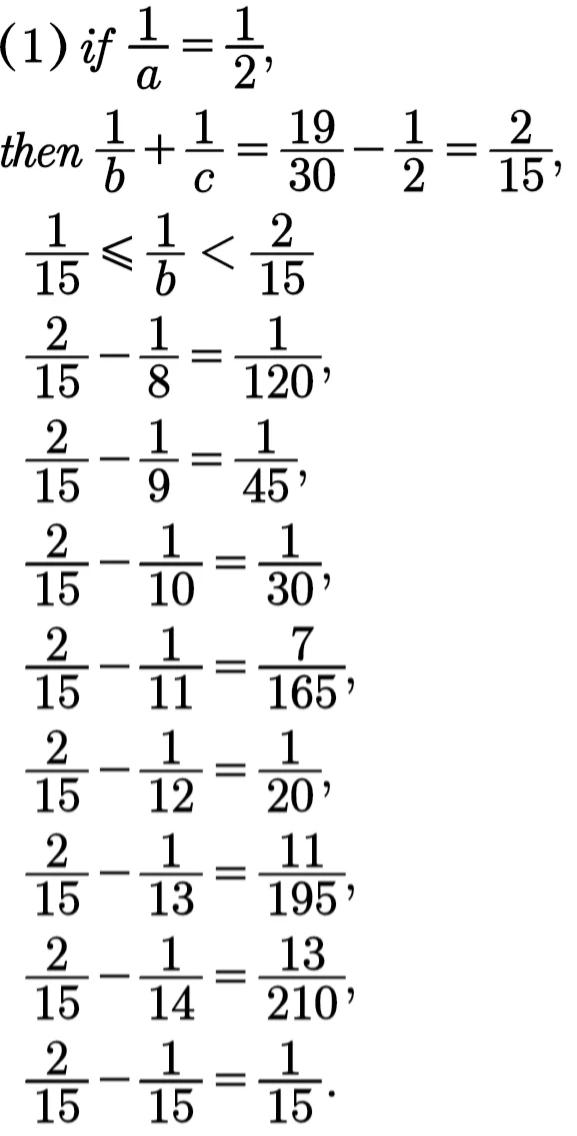
所得的八个差,只有五个是单位分数,由此可得符合题意的五种填法:

答案1
(2)当a分之1=⅓时,较大的加数b分之1应小于10分之3,又不小于(10分之3÷2=3/20)20分之3,即,

b 可能是4、5和6。试算:

这样,又得到两种符合题意的填法:

答案2
(3)当a分之1=¼时,较大的加数b分之1应小于60分之23,又不小于(60分之23÷2=23/120)120分之23,即

b 可能是4和5。试算:

所得的差都不是单位分数,找不到新的符合题意的填法。
所以这道题一共有7种填法。

7种填法即图片:答案1和答案2。