缺失数据处理一直是机器学习实践中的难点。MICE(Multivariate Imputation by Chained Equations)作为一种基于迭代思想的插补框架,可以处理复杂缺失值问题。因为它不是简单地用均值或中位数填补空缺,而是通过构建后验分布来建模不确定性,这种处理方式在统计学上更为严谨。
但MICE的学习曲线优点陡峭,迭代机制和模型依赖特性也让不少人望而却步,所以本文会通过PMM(Predictive Mean Matching)和线性回归等具体方法,拆解MICE的工作原理,同时对比标准回归插补作为参照。
MICE的基本概念插补方法大致可以分三类:统计方法(均值、中位数、众数)、基于模型的方法(KNN、回归插补、GAIN等)、以及时间序列特有的前向后向填充。MICE属于模型方法,但它的实现路径更复杂——通过迭代式预测来逐步逼近真实分布。
整个流程如下图所示:
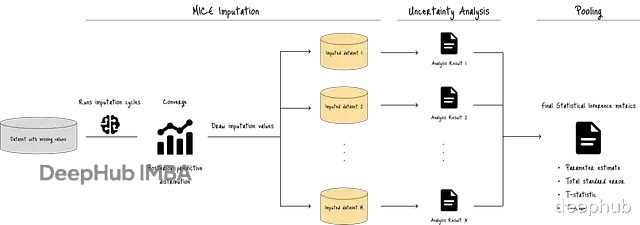
MICE首先运行多轮插补循环,用预测模型生成目标变量的后验分布。接着从这个分布中反复抽样(比如M次),生成多个版本的完整数据集。每个数据集的插补值都不相同,这种变异性是MICE的核心价值所在。
最后通过不确定性分析和池化(pooling),得到汇总的统计指标:池化参数估计、总标准误差、t统计量和p值。这些指标量化了缺失值带来的不确定性,帮助判断插补结果是否足够可靠。
链式预测的逻辑MICE的关键在于"链式"二字。假设有个简单数据集,包含Income(X1)和Age(X2)两个特征,都存在缺失。
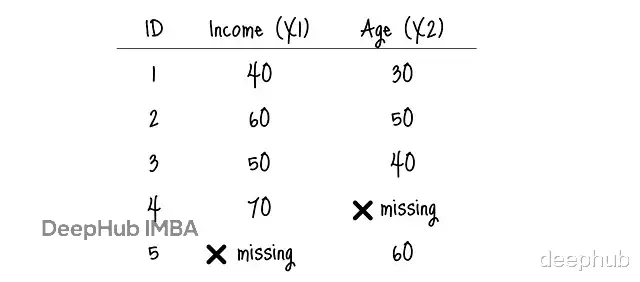
标准回归插补会直接用学到的函数填补空白:
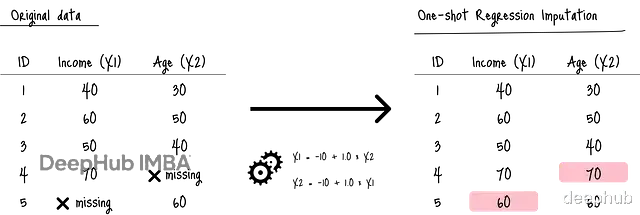
因为模型只在残缺的数据上训练,插补结果难免带有很大的偏差。
而MICE采取的策略不同:

它先用均值之类的粗略值填充所有空缺(浅粉色),然后用包括这些初值在内的"完整"数据去改进插补(深粉色)。这个过程会重复多轮,直到插补值趋于稳定,或者说就是收敛了。
MAR假设的限制MICE强依赖MAR(Missing At Random)假设——数据缺失与否只和已观测值相关,斌且给这个前提很严格的。
如果数据属于MCAR(完全随机缺失),用简单方法就够了。如果是MNAR(非随机缺失,比如高收入者故意不填收入),MICE效果会打折扣需要考虑自编码器或领域特定模型。
适用场景MICE的优势在于:
迭代过程提供了有效的不确定性估计,比一次性插补准确;能捕捉多变量之间的复杂依赖关系;利用其他变量信息,减少插补偏差
但代价也明显:计算慢、实现复杂、受底层模型假设约束(比如线性假设)。
所以使用MICE选对场景很重要:
多个变量都有缺失,且彼此关联;数据类型混杂(连续型和分类变量都有);缺失率比较高,达到10%以上,简单方法会引入明显偏差。
临床试验和公共卫生调查就是典型应用,这些领域对无偏估计要求极高。
算法机制分解按照图A,MICE分五步:
1、用占位符初始化
2、建模后验分布并采样
3、迭代至收敛
4、重复生成多个数据集
5、不确定性分析和池化
我们一步一步来介绍。
初始插补第一步用均值或中位数填充所有缺失位置。
形式化表示:
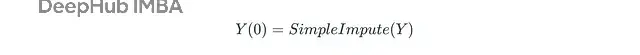
这里Y是包含P个变量的数据集,Y(t)代表第t轮迭代的状态。插补前Y包含观测值和缺失值两部分。
后验分布与采样接下来是核心步骤:
训练预测模型
构建目标变量的条件后验分布
从分布中抽样
假设目标变量是X1(包含缺失),用列索引j和迭代轮次t来表示:
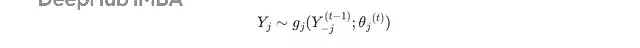
其中Y_j是观测值,Y_j^{(t−1)}是上一轮的插补结果,g_j是后验分布,θ_j(t)是模型参数。
后验分布的形式取决于预测模型。
回归任务常用这几种:
正态线性回归:从正态分布采样,均值是预测值μ_i^(t),方差σ_j^2(t)来自贝叶斯框架。
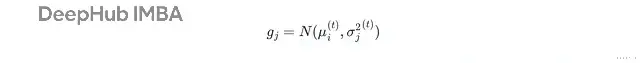
带Bootstrap的正态线性回归:分布形式相同,但参数从自助法样本中估计。
PMM(预测均值匹配):先用线性回归生成预测均值,然后从"捐赠者池"中随机抽取实际观测值。捐赠者池由预测均值最接近的k个样本组成,类似KNN的思路。
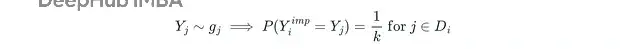
分类任务则用:
逻辑回归:从伯努利分布(二分类)或多项分布(多分类)中采样。
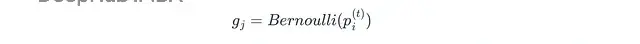
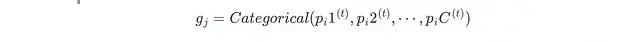
比例优势模型:参数量更少,因为所有截断点共享一组斜率系数。
迭代收敛MICE会对所有缺失变量依次执行上述步骤,直到所有值都收敛。
比如数据集有4个目标变量(j = 0, 1, 2, 3),MICE会顺序处理:先给j=0建模采样,然后j=1以此类推。这种顺序确保了链式依赖——j=0的插补结果会用在j=1的预测中。
生成多数据集单次收敛还不够。MICE会把整个迭代循环跑多遍(比如20次),每次都从后验分布随机采样,生成多个版本的完整数据集。这些数据集的插补值各不相同,正是这种变异性让不确定性量化成为可能。
不确定性分析与池化最后对所有插补数据集做相同的统计分析。
比如说研究年龄和BMI对胆固醇的影响,用OLS线性回归建模:
Cholesterol ∼ β_0 + β_1·Age + β_2·BMI + ϵ
每个插补数据集D(m)会得到一组系数估计θ^_m和方差协方差矩阵U_m。
Rubin规则把这些结果合并。比如参数θ的池化估计是M个估计值的均值:
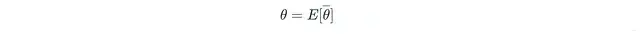
估计误差(池化标准误差)由总方差决定:
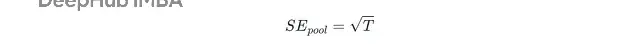
总方差分解为插补内方差和插补间方差:
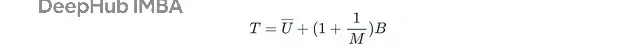
Uˉ反映采样变异性,B量化插补引入的额外不确定性,M是数据集数量。有了这些,就能构建置信区间和p值。
代码用合成数据集演示回归任务。数据包含10000个样本,三个特征X1、X2、Y。
对比三种方法:
MICE + PMM
MICE + 正态线性回归
标准回归插补(基线)
结构化缺失值先把各种形式的缺失标记统一成np.nan。Pandas默认不识别空格、"NA"、"?"这类非结构化标记。
import pandas as pd import numpy as np def structure_missing_values(df: pd.DataFrame, target_cols: list = []) -> pd.DataFrame: target_cols = target_cols if target_cols else df.columns.tolist() # list up unstructured missing val options unstructured_missing_vals = ['', '?', ' ', 'nan', 'N/A', None, 'na', 'None', 'none'] # structure structured_nan = { item: np.nan for item in unstructured_missing_vals } structured_df = df.copy() for col in target_cols: structured_df[col].replace(structured_nan) return structured_df df_structured = structure_missing_values(df=original_df)
分析缺失类型用t检验判断缺失模式。比较有无缺失两组样本在其他变量上的均值差异。
from scipy import stats def assess_missingness_diagnostics(df, target_variable='X1', missingness_type='mcar'): # create a missingness indicator df_temp = df.copy() df_temp['is_missing'] = df_temp[target_variable].isna().astype(int) observed_vars = [col for col in df_temp.columns if col not in [target_variable, 'is_missing']] # compare means of observed variables (x2, y) between 1) group_observed (x1 observed) and 2) group_missing (x1 missing) for var in observed_vars: # create the groups group_observed = df_temp[df_temp['is_missing'] == 0][var] group_missing = df_temp[df_temp['is_missing'] == 1][var] # check if enough samples exist in both groups if len(group_missing) < 2 or len(group_observed) < 2: continue # perform two-sample t-test to compute the mean difference _, p_value = stats.ttest_ind(group_observed.dropna(), group_missing.dropna()) mean_obs = group_observed.mean() mean_miss = group_missing.mean() # rejection of h0 (equal means) suggests missingness depends on the observed variable if p_value < 0.05: print(f" -> conclusion: mar or mnar because means are statistically different.") else: # failure to reject h0 suggests independence print(f" -> conclusion: mcar because means are not statistically different.") assess_missingness_diagnostics( df=df_structured, target_variable='X1', missingness_type='mar' )
结果显示X2和Y在两组间均值显著不同(p<0.05),符合MAR或MNAR特征。
实践中缺失类型往往模糊,可以试多种方法再比较泛化效果。
定义插补器确认适用性后,用Scikit-learn的IterativeImputer配置MICE。
PMM版本:
from sklearn.impute import IterativeImputer imputer_mice_pmm = IterativeImputer( estimator=PMM(), # pmm max_iter=10, # num of cycles initial_strategy='mean', # initial imputation val random_state=42, # for reproducibility )
自定义PMM估计器:
import numpy as np from sklearn.linear_model import LinearRegression from sklearn.base import BaseEstimator, RegressorMixin # implement a custom pmm estimator class PMM(BaseEstimator, RegressorMixin): def __init__(self, k: int = 5, base_estimator=LinearRegression()): self.k = k # k-neigbor self.base_estimator = base_estimator def fit(self, observed_X, observed_y): self.base_estimator.fit(observed_X, observed_y) # store the observed data self.X_donors = observed_X.copy() self.y_donors = observed_y.copy() # predict the means for all observed donors self.y_pred_donors = self.base_estimator.predict(self.X_donors) return self # core pmm logic of sampling val from the k nearest neighbors of observed data. x has missing vals def predict(self, X): # predict the mean for the missing data (recipients) y_pred_recipients = self.base_estimator.predict(X) imputed_values = np.zeros(X.shape[0]) # perform pmm for each recipient (row in x) for i, pred_recipient in enumerate(y_pred_recipients): # compute the absolute difference between the recipient's predicted mean and all the donor's predicted means. diffs = np.abs(self.y_pred_donors - pred_recipient) # get the indices that correspond to the k smallest differences (k nearest matches) nearest_indices = np.argsort(diffs)[:self.k] # taking k indices plus 1 to avoid an exact match of the imputed val from the prev round # randomly sample an observed value from the k nearest neighbors (donor_pool) donor_pool = self.y_donors[nearest_indices] imputed_value = np.random.choice(donor_pool, size=1)[0] imputed_values[i] = imputed_value return imputed_values ## func for IterativeImputer compatibility def _predict_with_uncertainty(self, X, return_std=False): if return_std: return self.predict(X), np.zeros(X.shape[0]) # pmm is semi-parametric. set standard deviation = 0 return self.predict(X)
库里的KNeighborsRegressor也能实现类似功能。
线性回归版本:
用BayesianRidge确保生成不同的插补值:
from sklearn.impute import IterativeImputer from sklearn.linear_model import BayesianRidge imputer_mice_lr = IterativeImputer( estimator=BayesianRidge(max_iter=500, tol=1e-3, alpha_1=1e-10, alpha_2=1e-10, lambda_1=1e-10, lambda_2=1e-10), max_iter=10, initial_strategy='mean', random_state=42, sample_posterior=True # add random noise drawn from the posterior distribution to the prediction. )
执行插补迭代5次(M=5),每次生成一个完整数据集。
import pandas as pd from sklearn.impute import IterativeImputer def run_mice_imputation(df: pd.DataFrame, imputer: IterativeImputer, M: int = 5) -> list: # iteration imputed_datasets= [] # subject to analysis and pooling later imputed_values_x1 = {} missing_indices_x1 = df[df['X1'].isna()].head(3).index.tolist() for m in range(M): # setup imputer for each interation (unique random state controls the numpy seed for pmm's sampling) setattr(imputer, 'random_state', m) # impute df and convert generated array to pandas df df_m = pd.DataFrame(imputer.fit_transform(df), columns=df.columns) # recording imputed_datasets.append(df_m) imputed_values_x1[m] = df_m['X1'].loc[missing_indices_x1].tolist() # outputs - unique imputation values print("Imputed values across M datasets (True PMM - expecting variability):") print(f"imputed dataset 1 - the first three imputed values for X1: {[f'{x:.14f}' for x in imputed_values_x1[0]]}") print(f"imputed dataset 2 - the first three imputed values for X1: {[f'{x:.14f}' for x in imputed_values_x1[1]]}") print(f"imputed dataset 3 - the first three imputed values for X1: {[f'{x:.14f}' for x in imputed_values_x1[2]]}") print(f"imputed dataset 4 - the first three imputed values for X1: {[f'{x:.14f}' for x in imputed_values_x1[3]]}") print(f"imputed dataset 5 - the first three imputed values for X1: {[f'{x:.14f}' for x in imputed_values_x1[4]]}") return imputed_datasets
PMM结果:
imputed_datasets_mice_pmm = run_mice_imputation(df=df, imputer=imputer_mice_pmm, M=5)
5个数据集的X1插补值各不相同,体现了随机性:
imputed dataset 1: ['9.24212539359209', '8.86784044761337', '16.27959379662983']imputed dataset 2: ['10.67728456933526', '6.72710070935441', '8.84037515230672']imputed dataset 3: ['10.15359370564326', '6.72710070935441', '18.59563606925789']imputed dataset 4: ['10.78202129747172', '6.72710070935441', '8.84037515230672']imputed dataset 5: ['9.35638700644611', '5.15233963776858', '13.88818918534419']
线性回归结果:
imputed_datasets_mice_lr = run_mice_imputation(df=df, imputer=imputer_mice_lr, M=5)
同样生成了5组不同的插补值:
imputed dataset 1: ['12.21062281693754', '9.96558458658052', '12.49501000922409']imputed dataset 2: ['8.71573023588752', '10.85416071007341', '12.35300502646557']imputed dataset 3: ['12.72459653377737', '8.71106811173562', '11.99063594937416']imputed dataset 4: ['9.73654929041454', '3.72657966114651', '12.08960122126962']imputed dataset 5: ['8.59526280022813', '12.78831127091796', '12.39797242039489']
池化分析对5个数据集做统计推断,用Rubin规则合并结果。
import numpy as np import statsmodels.formula.api as smf from scipy.stats import t def perform_analysis_and_pooling(imputed_datasets, target_param='X1'): m = len(imputed_datasets) estimates = [] # theta_m variances = [] # within-imputation variance u_m # 1. analysis - run the model on each imputed dataset for i, df_m in enumerate(imputed_datasets): # ols model model = smf.ols(formula='Y ~ X1 + X2', data=df_m).fit() # extract the estimate (theta_m) and its variance (u_m) for the target parameter estimate = model.params[target_param] variance = model.bse[target_param]**2 estimates.append(estimate) variances.append(variance) # 2. pooling w rubin's rules # pooled point estimate (theta_bar) theta_bar = np.mean(estimates) # within-imputation variance (u_bar) u_bar = np.mean(variances) # between-imputation variance (b) b = (1 / (m - 1)) * np.sum([(est - theta_bar)**2 for est in estimates]) # total variance (t) t_total = u_bar + (1 + (1 / m)) * b # total standard error (se) se_pooled = np.sqrt(t_total) # relative increase in variance (riv) and degrees of freedom (v) riv = ((1 + (1 / m)) * b) / u_bar v_approx = (m - 1) * (1 + (1 / riv))**2 # confidence interval t_critical = t.ppf(0.975, df=v_approx) ci_lower = theta_bar - t_critical * se_pooled ci_upper = theta_bar + t_critical * se_pooled print("\n--- pooled results using rubin's rules ---") print(f"pooled estimate ({target_param}): {theta_bar:.10}") print(f"within variance (u_bar): {u_bar:.10}") print(f"between variance (b): {b:.10f}") print(f"total variance (t): {t_total:.10}") print(f"pooled standard error: {se_pooled:.10}") print(f"relative increase in variance (riv): {riv:.10}") print(f"degrees of freedom (approx): {v_approx:.2f}") print(f"95% ci: [{ci_lower:.10}, {ci_upper:.10}]") return theta_bar, se_pooled, t_total, v_approx
PMM池化结果:
X1系数估计2.021,95%置信区间[1.954, 2.087]。相对方差增幅(RIV)仅5.7%,说明插补引入的不确定性很小。
pooled estimate (X1): 2.020731625within variance (u_bar): 0.001079913886between variance (b): 0.0000517265total variance (t): 0.001141985746pooled standard error: 0.0337932796relative increase in variance (riv): 0.05747852707degrees of freedom (approx): 1353.9295% ci: [1.95443875, 2.087024499]
线性回归池化结果:
X1系数2.029,置信区间[1.963, 2.096],RIV约6.8%,同样在可接受范围。
pooled estimate (X1): 2.029474175within variance (u_bar): 0.001082280232between variance (b): 0.000060931total variance (t): 0.001155397613pooled standard error: 0.03399114021relative increase in variance (riv): 0.06755864026degrees of freedom (approx): 998.8195% ci: [1.962771936, 2.096176414]
两种方法的不确定性都控制得不错。
模型评估在每个插补数据集上训练SVR(支持向量回归),平均MSE作为最终指标。
from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler from sklearn.compose import ColumnTransformer from sklearn.pipeline import Pipeline from sklearn.svm import SVR from sklearn.metrics import mean_squared_error mse_train_mice_pmm_list = [] mse_val_mice_pmm_list = [] for i, df in enumerate(created_datasets): # create X, y y = df['Y'] X = df[['X1', 'X2']] # create train, val, test datasets test_size, random_state = 1000, 42 X_tv, X_test, y_tv, y_test = train_test_split(X, y, test_size=test_size, shuffle=True, random_state=random_state) X_train, X_val, y_train, y_val = train_test_split(X_tv, y_tv, test_size=test_size, shuffle=True, random_state=random_state) # preprocess num_cols = X.columns num_transformer = Pipeline(steps=[('scaler', StandardScaler())]) preprocessor = ColumnTransformer(transformers=[('num', num_transformer, num_cols),], remainder='passthrough') X_train = preprocessor.fit_transform(X_train) X_val = preprocessor.transform(X_val) X_test = preprocessor.transform(X_test) # train the model model = SVR(kernel="rbf", degree=3, gamma='scale', coef0=0, tol=1e-5, C=1, epsilon=1e-5, max_iter=1000) model.fit(X_train, y_train) # inference y_pred_train = model.predict(X_train) mse_train = mean_squared_error(y_pred_train, y_train) y_pred_val = model.predict(X_val) mse_val = mean_squared_error(y_pred_val, y_val) # recording mse_train_mice_pmm_list.append(mse_train) mse_val_mice_pmm_list.append(mse_val) # final performance metric that accounts for imputation uncertainty. pooled_mse_train_mice_pmm = np.mean(mse_train_mice_pmm_list) pooled_mse_val_mice_pmm = np.mean(mse_val_mice_pmm_list) print(f'\nfinal performance - train mse: {pooled_mse_train_mice_pmm:.6f}, val mse: {pooled_mse_val_mice_pmm:.6f}')
对比结果:
MICE + PMM:训练394.14,验证368.20
MICE + 线性回归:训练331.43,验证308.42
回归插补:训练412.05,验证383.25
两种MICE方法都显著优于基线。其中线性回归版本表现最佳,验证MSE降到308.42。
原因可能有两点:一是线性回归模型精准捕捉了数据关系;二是PMM的随机采样引入了额外噪声,虽然理论上更稳健但在这个数据集上反而增加了误差。
小结MICE在处理复杂缺失数据时有明显优势,尤其是需要无偏推断的场景。实验表明它确实能提升模型表现,比单次回归插补效果更好。
不过实践中还有优化空间:估计器选择、迭代次数、收敛标准都会影响最终效果。另外MAR假设的适用性判断也需要仔细评估,盲目套用可能适得其反。
缺失数据处理本身就是个权衡问题——计算成本、模型复杂度、统计有效性之间需要找平衡点。MICE提供了一种严谨的解决方案,但不是万能钥匙,要结合具体问题具体分析。
完整代码:
https://avoid.overfit.cn/post/e54f988c93df418db5ccbd1d37a92007
作者:Kuriko Iwai