数学是一个充满了神奇形状、图案和公式的世界，它们既令人好奇又令人愉快。伯努利双纽线（Lemniscate of Bernoulli）就是这样一种令人着迷的几何形状，它以瑞士数学家雅各布·伯努利的名字命名。在这篇文章中，我们将深入探讨伯努利双纽线的迷人世界，了解它的定义、性质以及数学原理。

伯努利双纽线的发展历史可以追溯到17世纪，它在数学史上占有重要地位。这条曲线最早由瑞士数学家雅各布·伯努利（Jacob Bernoulli）于1694年发现。伯努利双纽线实际上是卡西尼椭圆（Cassini oval）的一个特殊情况。卡西尼椭圆是由意大利数学家乔瓦尼·多梅尼科·卡西尼（Giovanni Domenico Cassini）研究的。

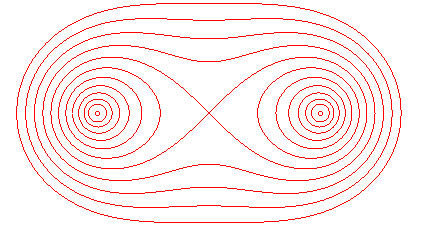
卡西尼椭圆

在几何学中，卡西尼椭圆是一种四次平面曲线，其定义为平面上与两个固定点（焦点）距离之积保持恒定的点的轨迹。这与椭圆形成对比，椭圆是距离之和保持恒定，而非距离之积。当使用的多项式的次数为2时，卡西尼椭圆是多项式双纽线的特殊情况。17世纪末，卡西尼认为太阳绕地球运行在这些椭圆之一上，地球位于椭圆的一个焦点处（需要引用）。其他名称包括卡西尼椭圆、卡西尼曲线和卡西尼椭圆。

卡西尼椭圆是描述在平面上与两个给定焦点 F1 和 F2 的距离之积等于常数 b^2 的点的集合。当焦点间的距离等于 2b 时，卡西尼椭圆就会变成伯努利双纽线。

在1694年，瑞士数学家雅各布·伯努利在研究卡西尼椭圆时发现了这个特殊情况。他注意到，在这个特定条件下，卡西尼椭圆形成了一个连通的、类似于无限符号（∞）的形状，我们现在称之为伯努利双纽线。

极坐标定义

伯努利双纽线可以用极坐标来定义。给定一个固定点O，双纽线的方程为

在这里，r 是从点 O 到曲线上某一点的距离，a 是一个决定双纽线大小的常数，θ 是正 x 轴与连接点 O 到曲线上点的直线之间的夹角。

性质

让我们深入了解伯努利双纽线的一些迷人特性：

对称性：双纽线在 x 轴和 y 轴方向上都具有反射对称性，并具有4阶旋转对称性，这意味着当旋转90度时，它保持不变。

有界面积：伯努利双纽线所围成的面积可以用以下积分计算：

弧长：可以使用椭圆积分计算双纽线的一个环的长度，得到以下公式：

E(k²) 是第二类完全椭圆积分，且 k² = 1/2。

应用

许多数学家对伯努利双纽线进行了深入研究，发现了许多有趣的性质。

在18世纪，法国数学家、微分几何学的奠基人之一加斯帕尔·莫尔讷（Gaspard Monge）对伯努利双纽线进行了深入研究，通过研究伯努利双纽线的切线和法线，提供了对双纽线几何性质的更深入的理解。这些性质在曲线的微分几何描述中具有重要作用，例如曲率、挠率等。这些研究对于理解曲线的局部性质以及在物理和工程学中的应用具有重要意义。

在19世纪，德国数学家卡尔·威尔斯特拉斯（Karl Weierstrass）发现了伯努利双纽线与椭圆函数的联系。威尔斯特拉斯研究了一种名为威尔斯特拉斯椭圆函数的特殊函数。这些椭圆函数是周期性的复函数，用于描述复平面上的周期性结构。威尔斯特拉斯发现，这些椭圆函数可以用于表示伯努利双纽线，从而在复分析和代数几何中建立了双纽线的数学框架。

另外，伯努利双纽线在物理学和工程学中也有一定的应用。例如，在电磁场中，带电粒子在特定条件下沿伯努利双纽线运动。双纽线的研究也为研究其他曲线、表面和高维空间中的几何结构奠定了基础。

总之，伯努利双纽线自17世纪以来在数学、物理学和工程学等领域发展演变，吸引了无数学者对其进行深入研究。这条曲线及其丰富的性质和应用证明了其在数学史上的重要地位。