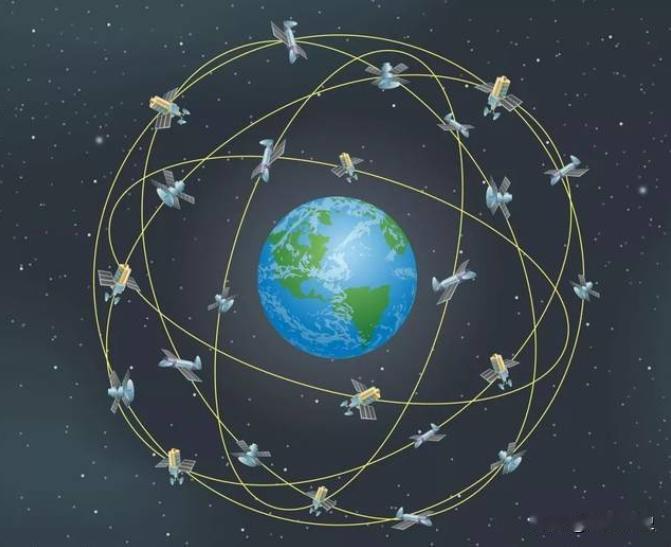
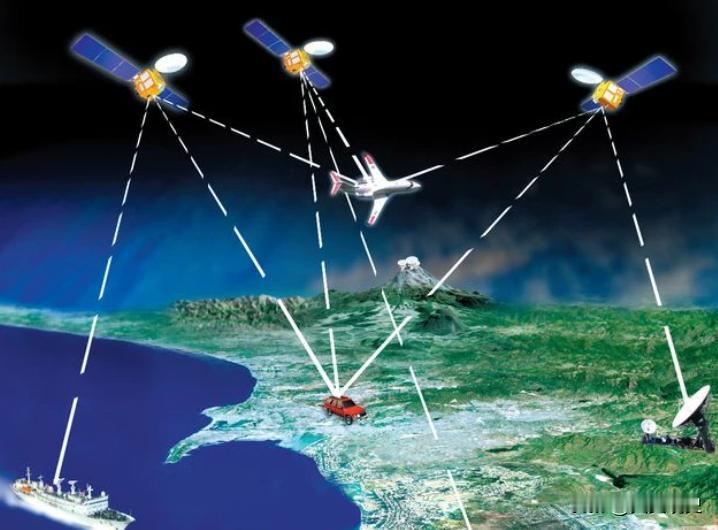
开普勒定律的应用 开普勒定律是描述行星运动的重要定律,被广泛应用于天文学、航天学和导航学等领域。本文将从三个方面介绍开普勒定律的应用:第一,开普勒定律在行星运动中的应用;第二,开普勒定律在卫星轨道中的应用;第三,开普勒定律在导航系统中的应用。 一、行星运动 开普勒定律是描述行星运动的基本定律,它由德国天文学家约翰内斯·开普勒于17世纪发现。根据开普勒定律,行星绕太阳运动的轨道是一个椭圆,太阳处于椭圆的一个焦点上。 1)计算行星的轨道周期。根据开普勒第三定律,行星绕太阳运动的周期与它的轨道半长轴的三次方成正比。因此,如果已知行星的轨道半长轴,就可以用开普勒定律计算出它的轨道周期。这个应用非常重要,因为它可以帮助天文学家预测行星的位置和运动。 2)计算行星的轨道速度。根据开普勒第二定律,行星在它的轨道上离太阳的距离和它的速度成反比。因此,如果已知行星在轨道上的距离,就可以用开普勒定律计算出它的速度。这个应用也非常重要,因为它可以帮助天文学家了解行星的运动状态。 3)计算行星的轨道倾角。根据开普勒第一定律,行星绕太阳运动的轨道是一个椭圆,太阳处于椭圆的一个焦点上。这个焦点和轨道的中心之间的连线称为轨道长轴。轨道长轴与参考平面的夹角称为轨道倾角。如果已知行星的轨道长轴和轨道半短轴,就可以用开普勒定律计算出它的轨道倾角。这个应用可以帮助天文学家确定行星运动的轨道方向,从而更好地研究它的运动规律。 二、卫星轨道 开普勒定律还可以应用于卫星轨道的计算和设计。卫星是一种人造物体,需要被放置在一个特定的轨道上以完成其任务。 1)计算卫星的轨道高度。根据开普勒第三定律,卫星在轨道上的运动周期与它的轨道高度的三次方成正比。因此,如果已知卫星的轨道周期,就可以用开普勒定律计算出它的轨道高度。这个应用非常重要,因为它可以帮助工程师确定卫星的运行高度,从而更好地满足卫星的任务需求。 2)计算卫星的轨道速度。根据开普勒第二定律,卫星在轨道上的速度与它的轨道高度成反比。因此,如果已知卫星的轨道高度,就可以用开普勒定律计算出它的轨道速度。这个应用也非常重要,因为它可以帮助工程师确定卫星的运行速度,从而更好地满足卫星的任务需求。 3)计算卫星的轨道倾角。卫星轨道的倾角是指卫星轨道与地球赤道平面之间的夹角。根据开普勒第一定律,卫星在轨道上的运动轨迹是一个椭圆,地球位于椭圆的一个焦点上。这个焦点和轨道的中心之间的连线称为轨道长轴。如果已知卫星的轨道长轴和轨道半短轴,就可以用开普勒定律计算出它的轨道倾角。这个应用可以帮助工程师设计出更加稳定的卫星轨道,从而更好地完成卫星的任务需求。 三、导航系统 导航系统是一种用于确定位置和导航的系统,如GPS系统就是一种典型的导航系统。 1)计算卫星的位置。导航系统中的卫星是以一定的轨道运行的,为了确定用户的位置,需要知道卫星的精确位置。而根据开普勒定律,已知卫星在轨道上的运动状态和轨道参数,就可以计算出卫星的位置。 2)优化导航系统的性能。导航系统的精度和稳定性与卫星的运动状态和轨道参数有关。因此,通过对卫星轨道的精确计算,可以优化导航系统的性能。 四、开普勒定律在太空探测中的应用 1)计算行星和卫星的运动轨迹。在太空探测中,探测器需要准确地到达目标星球或卫星,因此需要预先计算它们的运动轨迹。而开普勒定律提供了一个精确的计算模型,可以帮助工程师计算出行星和卫星的运动轨迹,从而准确地规划探测器的轨迹和飞行路线。 2)研究星系和宇宙的结构。开普勒定律提供了一种了解行星、卫星和其他天体运动规律的方法,可以帮助科学家更好地研究星系和宇宙的结构。例如,通过观测行星的运动轨迹和周期,可以推算出行星的质量、密度和轨道参数等信息,从而更好地了解行星的特性和演化规律。 参考文献: 1. Armitage, P.J. (2010). Astrophysics of Planet Formation. Cambridge, UK: Cambridge University Press. 2. Brush, S.G. (1970). The Kinetic Theory of Gases: An Anthology of Classic Papers with Historical Commentary. New York: Dover Publications. 3. Murray, C.D., & Dermott, S.F. (1999). Solar System Dynamics. Cambridge, UK: Cambridge University Press.