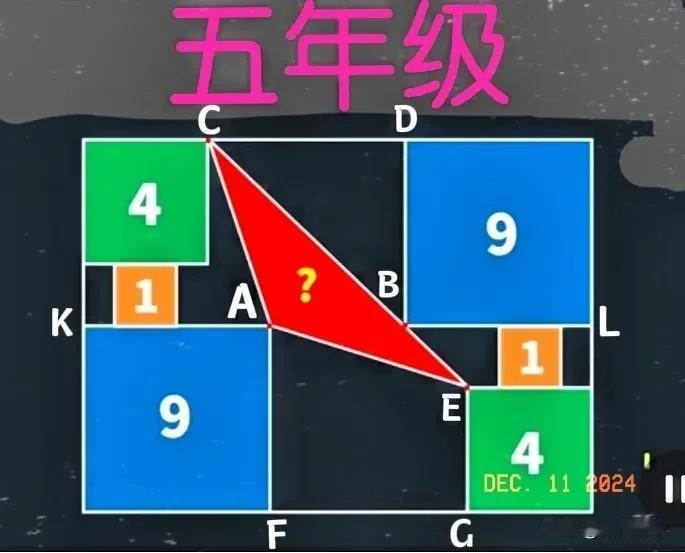
“全军覆没，几乎全体白卷！”考试一结束，很多孩子就向老师反映“题目缺少条件、无法求解”，不少家长也是这么认为的！这是一道小学五年级数学竞赛题：难度非常大，难在长方形的长未知！ 如图，一个长方形内有6个正方形，面积分别为1、4和9，求红色阴影三角形ACE的面积。 突破口：求线段CD和AB的长度！ ———————— 提示：说明△BCD为等腰直角三角形！ ①长方形的宽为1+2+3=6。 ②延长FA、与CD相交于点M，延长DB与FG相交于点N，则A、B分别为分别为长方形FMDN两边FM和DN的中点，即AB、AK、BL均在BL上。 ③过点E作BL的垂线EH，则BH=BL-HL=3-2=1=EH，从而BEH和BCD均为等腰直角三角形。故CD=3，AB=2。 ④S△ACE=S△ABC+S△ABE=2×3÷2+1×2÷2=4。 或 ④'过点E作FM的垂线EP，与DN相交于点Q，则长方形PMDQ的长PM=4、宽DM=AB=2，S△ACE=1/2S长方形PMDQ=4。 友友们，怎么看？欢迎留言分享！ 妙笔生花创作挑战 小学数学
秋风秋雨zwc
关键是证明AB的长度，BD等于3己知。因BE在两个正方形角上，根据己知条件是一个边长为1的正方形，所以其延长线段BC所构成三角形BCD为等腰直角三角形，因此可得AB为2，其它都好说了
用户10xxx48
4啊
正在输入
先证明CD=BD=3，再得出AB=2，红色面积=(2*3+2*1)/2=4
Locky
想了想，是缺少条件，因为两组正方形的距离不定，也就是长方形的长不定