数学是一个充满奇迹和惊喜的世界，在这个世界中，基数作为一种神秘的度量，探索着集合中元素数量的奥秘。自19世纪以来，基数已经从一个初步概念发展成为集合论的核心组成部分，不仅丰富了数学家们对无限集合的理解，还为计算机科学、信息论等领域提供了重要的基础知识。集合论创始人乔治·康托认为，研究无限集合的基数有助于理解数学中的许多问题，并称之为“数学的天堂”。

基数用于表示集合中元素的数量。它度量了一个集合的“大小”，并可用于比较和描述不同集合之间的大小关系。基数可以描述有限集合的大小，也可以描述无限集合的大小。

对于有限集合，基数是一个非负整数，表示集合中元素的个数。例如，集合 {2, 4, 6, 8, 10} 的基数是5，因为它包含 5 个元素。

对于无限集合，基数的描述较为复杂。无限集合可分为可数无限集合和不可数无限集合：

可数无限集合：与自然数集合（0, 1, 2, 3, ...）可以建立一一对应关系的集合。例如，整数集合和有理数集合。可数无限集合的基数称为阿列夫零（aleph-null），通常记为

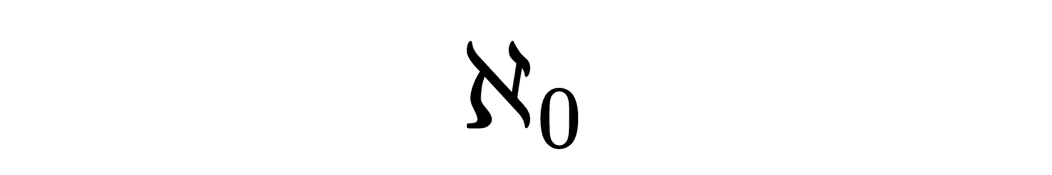
不可数无限集合：无法与自然数集合建立一一对应关系的集合。例如，实数集合（包括无理数和有理数）。不可数无限集合的基数大于阿列夫零。

两个集合具有相同的基数，当且仅当它们之间存在一一对应关系。一一对应关系是指集合 A 中的每个元素都可以唯一地与集合 B 中的一个元素对应，反之亦然。

有理数与自然数一一对应

那么如何证明有理数可以和自然数建立一一对应关系呢？

为了证明有理数可以与自然数建立一一对应关系，我们需要找到一种方法将有理数与自然数进行配对。这里，我们将介绍一种可能的方法。

有理数是可以表示为两个整数（分子和分母）比值的数。我们可以通过将有理数排列成一个无限表格，并按照特定顺序遍历表格中的元素来建立有理数与自然数之间的一一对应关系。首先，我们构建一个表格，其中行和列的索引都是正整数，表格中的每个元素表示为行索引除以列索引（既有理数）：

然后，我们按照对角线顺序遍历表格中的元素。这种顺序称为“对角线顺序”：

从左上角的 1/1 开始，我们按照对角线顺序遍历表格。这意味着我们沿着从左下到右上的对角线移动。以下是对角线顺序的前几个元素：

首先，我们访问 1/1；

接着，我们访问第二条对角线：1/2 和 2/1；

然后是第三条对角线：3/1，2/2 和 1/3；

继续访问第四条对角线：1/4，2/3，3/2 和 4/1；

以此类推。

对角线顺序是：

1/1, 1/2, 2/1, 3/1, 2/2, 1/3, 1/4, 2/3, 3/2, 4/1, ...

然后我们需要去除重复的有理数并建立与自然数的一一对应关系。例如，2/2 和 1/1 是相同的有理数。同时，我们还要注意化简分数。在这个例子中，我们可以得到以下的对应关系：

通过这种方式，我们可以将有理数与自然数建立一一对应关系，证明有理数集合是可数的。

实数无法与自然数建立一一对应关系

为了证明实数无法与自然数建立一一对应关系，我们可以使用康托尔的对角线论证（Cantor's diagonal argument）。这是一种反证法，即通过假设实数与自然数之间存在一一对应关系，然后找到一个与已知对应关系中的任何实数都不匹配的新实数，从而得出矛盾。

假设实数集合（在此，我们考虑[0,1)区间内的实数）与自然数集合可以建立一一对应关系。那么，我们可以将[0,1)区间内的实数列成一个无穷表格，每个实数用它的十进制表示，如下：

注意，上面的表格包含了0到1的所有实数。

然后，我们再构造一个新的实数，其小数部分的每位数字都与对角线上的数字不同。为此，我们选择一个与 a11 不同的数字作为新实数的第一位，一个与 a22 不同的数字作为新实数的第二位，以此类推。例如，如果对角线上的数字是 1，我们可以选择 2；如果对角线上的数字是非 1 的任何其他数字，我们选择 1。新构造的实数如下所示（红色方框内的）：

根据构造方法，新实数的第 n 位与表格中第 n 行实数的第 n 位不同。这意味着，新实数与表格中的任何实数都不相同，与我们的假设矛盾，即实数集合与自然数集合之间存在一一对应关系。因此，我们得出结论：实数无法与自然数建立一一对应关系，实数集合是不可数的。

连续统假设（Continuum Hypothesis，简称 CH）是一个关于集合论中无限集合基数的假设。它是由德国数学家乔治·康托尔（Georg Cantor）提出的，是集合论中的一个著名问题。

连续统假设的陈述如下：

不存在一个集合，其基数大于自然数集合的基数（阿列夫零，ℵ₀）且小于实数集合的基数（用c表示）。

用数学符号表示为：不存在一个集合 X，满足，

换句话说，连续统假设认为不存在一个集合，它的大小介于可数无限集合（如自然数、整数和有理数集合）和实数集合之间。

值得注意的是，连续统假设既没有被证明为真，也没有被证明为假。哥德尔（Kurt Gödel）和科恩（Paul Cohen）分别在20世纪30年代和60年代证明了，在标准的公理集合论（ZFC，Zermelo-Fraenkel集合论，带选择公理）中，连续统假设既不可证也不可否证。这意味着连续统假设在目前公认的集合论框架中既可以被接受为真，也可以被接受为假，取决于数学家选择的基本公理。

基数在现代数学和其他科学领域中有广泛的应用。在计算机科学中，基数的概念用于理解数据结构和算法的性能。当处理大量数据时，了解数据集的基数有助于选择适当的排序、查找和存储算法。例如，将具有不同基数的数据集进行排序时，可能需要采用不同的排序算法，以便在不同情况下实现最佳性能。

在信息论中，基数扮演着重要角色，尤其是在处理离散信源和信道容量的问题时。理解信源或信道的基数有助于确定有效的编码和解码策略，从而实现高效的信息传输和存储。此外，基数在香农熵的计算中也起到关键作用，香农熵可以用于量化信息的不确定性。

基数在概率论和统计学中的应用也非常广泛。计算概率空间中事件的可能性、分布函数的定义和参数估计等都与基数有关。理解基数有助于分析随机过程和统计模型的性质，以及为统计推断提供理论基础。

在量子信息科学中，基数的概念用于描述量子系统的状态空间。量子比特（qubit）是量子信息科学的基本单元，其状态空间具有两个基本状态，因此具有基数2。类似地，量子多比特系统具有更大的基数，这对于描述量子计算和量子通信等领域的问题具有重要意义。