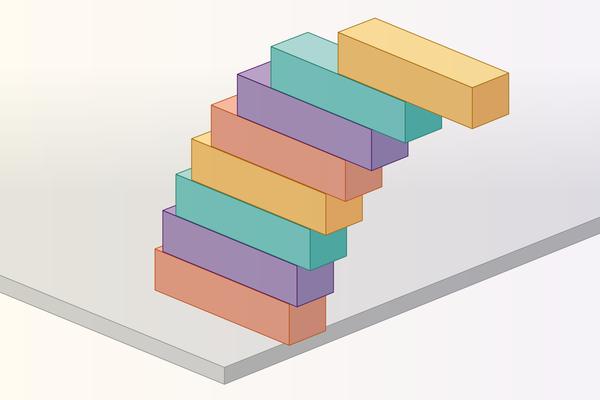
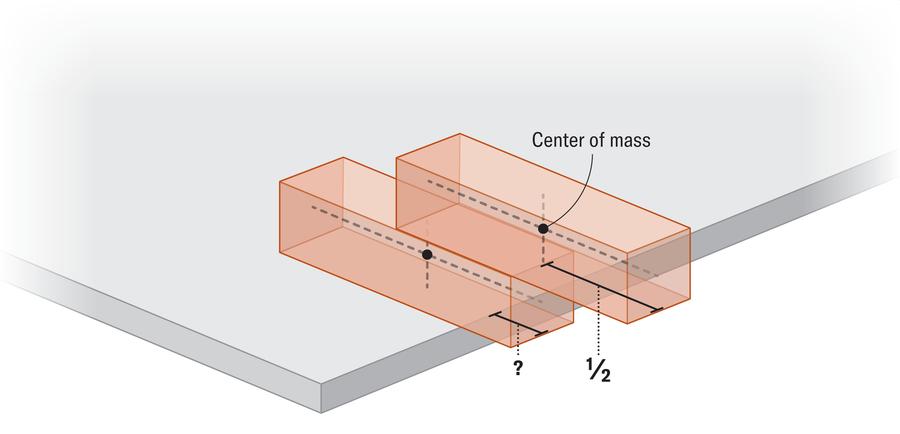
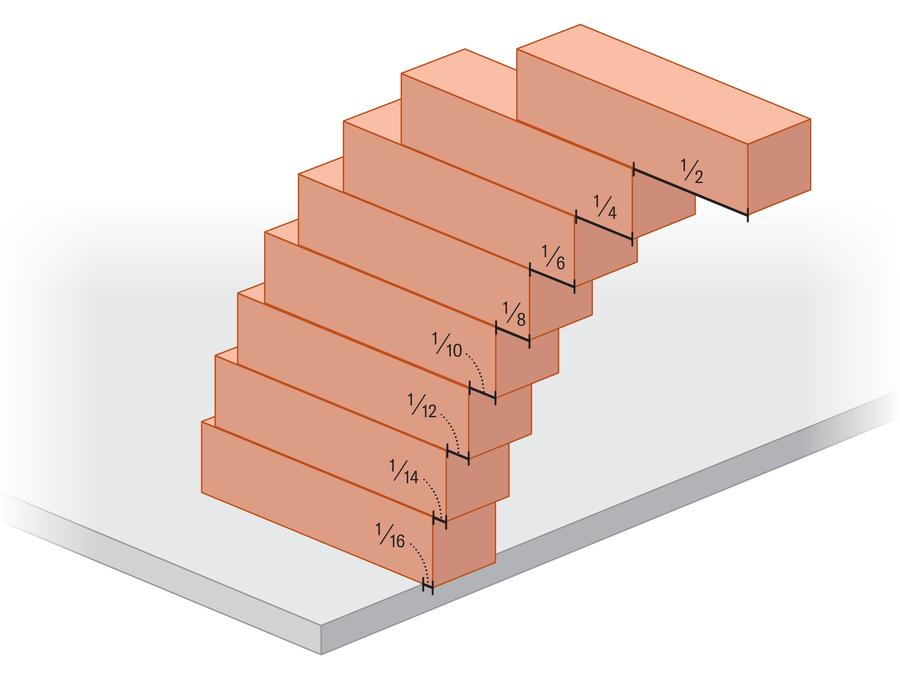
用一堆儿童积木,就能搭出一座跨越大峡谷的桥? 这听起来像是天方夜谭,不过让我们先思考一下:两块积木叠在一起,最上面的那块能伸出桌沿多远才不会倒?如果积木越来越多,这个悬空距离能达到多长呢?【图1】 答案可能会让你吓一跳:这座积木桥可以无限延伸。没错,不用胶水,不用任何支撑,纯靠积木巧妙的堆叠就能实现! 不过要注意一个注意关键词:“理论上”。现实中,积木不规则、风吹草动、还有积木本身的重量,都会让这种无限延伸的积木桥变成不可能的任务。 但这不妨碍我们来解开这个看似反常识的谜题。这背后的秘密,藏在数学的调和级数和物理的重心概念里。 任何物体都有重心,它可视为全部重量集中的平衡点。只要重心位于桌面正上方,物体就能保持平衡。 拿积木来说,我们可以把每块积木都看作是完全相同且密度均匀的,因此每块积木的重心都在正中央。 而在增加积木时,必须考虑整座塔的重心变化。为简化计算,让我们假设每块积木长度为1,质量为1: 当我们有两块积木时,最上面那块可以伸出1/2的长度,而底层积木只能悬空1/4长度,此时两积木系统的合重心恰好平衡于桌沿正上方。【图2】 随着积木增加,规律逐渐显现:顶层积木悬空1/2,第二层1/4,第三层1/6,第四层1/8,后续依次为1/10、1/12等。 要计算积木的最大悬空距离,需累加所有悬空量。也就是说,10块积木可悬空1/2+1/4+1/6+1/8+1/10+1/12+1/14+1/16+1/18+1/20≈1.464个积木长度。【图3】 但悬空极限是多少呢?这需要将无限递减的项相加。这种模式与调和级数惊人相似,后者将所有正整数的倒数相加:1+1/2+1/3+1/4+1/5+...直至无穷。 仔细观察会发现积木悬空量正是调和级数各项的一半:1/2+1/4+1/6+1/8+1/10+... 微积分告诉我们,调和级数虽然增长得非常慢,但它最终会趋向无穷大。 既然积木的悬空量是调和级数的一半,那无穷大的一半,也依然是无穷大!所以,在理想状态下,积木桥真的可以无限延伸。 尽管我们没法真的造出一架无限延伸的桥,但你仍然可以用积木动手挑战一下:仅需4块积木,就能让顶层积木完全悬空于桌沿外(1/2+1/4+1/6+1/8≈1.042)。 不过,如果你真想搭一座跨越科罗拉多大峡谷的积木桥,那可能需要惊人的毅力和无数的积木。 要悬空两个积木长度,就需要31块积木;而即使有1亿块积木,也未必能悬空10个积木长度。 在超大尺度下,物理定律会终结数学家的游戏。但在重心与调和级数主宰的理想世界里,可能性确确实实是无限的。