开头我们先讲个故事:
在某个风和日丽的下午,小明正沉浸在他的数学书中,突然看到了一张神奇的图片。
那是一种奇特的形状,像瓶子却又不像。
它有个瓶颈,但这个瓶颈却不像一般的瓶子那样朝上,而是绕了一个弯,直接穿过瓶底,最终回到了瓶子的内部。
“这是什么奇怪的瓶子?”小明疑惑地问自己。
这么奇怪的瓶子是否存在这个世上呢?
没错,这就是今天我们要讲的主角 —— 克莱因瓶。
01 什么是克莱因瓶?
克莱因瓶是一个奇特的几何形状,属于数学中“拓扑学”的领域。要理解克莱因瓶,我们可以从简单的二维形状开始。
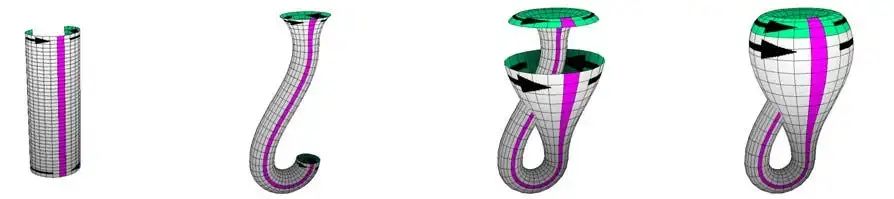
想象你有一张长方形的纸。
现在,我们先把纸的左边和右边相连,形成一个圆柱体。
接着,再把圆柱体的上下两端相连,你会得到一个“圆环”(数学上称作“环面”)。
但克莱因瓶比这个复杂得多。
它的形状可以视为把一个圆柱体的两个端面连接在一起,但不同的是,它的连接方式让这个瓶子既没有内部也没有外部——你可以沿着表面一直走,却永远不会遇到一个边界。

浸入三维空间中的克莱因瓶
换句话说,克莱因瓶只有一个面,没有“内外之分”。
更让人惊奇的是,克莱因瓶在三维空间中其实是无法“正常”构造的。
为什么呢?因为要把它的瓶颈接回瓶身,它必须在某个地方“穿越”自己的表面。
在现实生活中,我们用的克莱因瓶模型通常是在三维空间中“自相交”的版本,但在数学上,真正的克莱因瓶是在四维空间中才能完全不自相交地存在的。
02. 听不懂?再换个方式解释
听起来有点难懂对吧?那我们再用一个简单的故事来帮助理解。
有一天,小明进入了一个魔法世界。
在这个世界里,他发现了一条神奇的隧道。隧道的入口很普通,但当他走进去时,却发现自己并没有像想象中那样从另一端走出来。
相反,他惊奇地发现,自己回到了隧道的入口——这个隧道就像一条环形道路,绕了一圈又回到了起点。
“太不可思议了!”小明感叹道。
这个隧道其实就像克莱因瓶的表面一样,没有明确的内外之分,也没有边界,你走到哪里都像是回到了原点。
如果你能想象出一个封闭的隧道,但这个隧道的每一部分都能无缝连接,形成一个独立的空间——这就是克莱因瓶给我们带来的奇妙之处。
03. 克莱因瓶带给我们的启发
克莱因瓶不仅仅是一个数学中的奇怪形状,它还让我们重新思考了“内外”的概念,挑战了我们对空间和维度的直觉。
1、空间维度的拓展:克莱因瓶展示了我们在三维空间中难以实现的东西。它暗示着在更高维度中,可能存在一些我们难以想象的几何形状。
在数学中,克莱因瓶引导我们思考四维空间以及更高维度的拓扑结构。
2、打破常规思维:在日常生活中,我们习惯了“内”和“外”的概念,但克莱因瓶提醒我们,有些东西并不遵循常规逻辑。它让我们反思日常中看似简单的概念,在某些情况下可能并不适用。
3、拓扑学的奇妙世界:克莱因瓶是拓扑学中一颗璀璨的明珠。拓扑学是研究几何形状在变形过程中如何保持不变性质的数学领域。
通过克莱因瓶,我们看到了即使在不改变形状表面基本结构的情况下,也能产生如此奇妙的几何形态。
4、激发创造力:克莱因瓶这种看似不可能的几何体给了艺术家、工程师和科学家们无限的灵感。
它的形状被用在现代艺术中,甚至有人设计了实际的克莱因瓶形状的容器(尽管它们在三维空间中不是真正的克莱因瓶)。这种奇特的结构激发了人们对新形状、新结构的思考与创造。
数学不仅仅是关于数字和方程,它也是一种探索世界的方式。克莱因瓶就像是数学中的一扇窗,让我们窥见了另一个奇妙的世界。
这个瓶子本身或许难以用肉眼看到它的真实形态,但它让我们想象到了不一样的空间。
数学的魅力在于,它能够超越现实,带领我们进入一个由逻辑和规则构建的世界。
在这个世界里,克莱因瓶这样的形状揭示了隐藏在我们日常经验背后的奥秘。它提醒我们,现实并非一切,数学能够打开通往无限可能性的通道。
结语
克莱因瓶是一种非常特别的数学结构,它不仅让我们重新认识了几何形状,还让我们反思空间和维度的本质。
它不仅仅是一个瓶子,而是一扇通向未知的门。