反应动力学的基本理论，重点研究了电化学反应的能级电化学反应牵涉到Ox）或还原剂（Rd）之间的，因此这一反应与。图1是电极/电解液界面电子转移的能级-能态密度示意图。

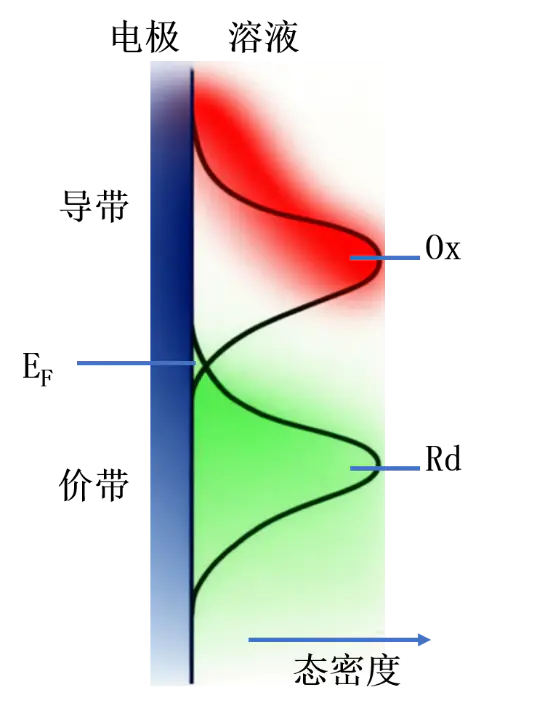
。外加于金属电极的电位将改变金属的Fermi能级，即改变电子的能量。

阴极极化F2（a）），使电子的能量升高，有利于还原反应的发生。则使E向下移动（图图2. 改变电极电位对电子转移的能量的影响。（a）阴极极化;（b）阳极极化。

电化学反应的电流-电位方程

Ox+ne–Rdc和RdNernst关系：

=φ⊖′/*C/C（2）

k，反应速率和反应电流分别为fi；后向反应（氧化反应或称为阳极反应）的速率常数为bv和aV=fOx0,t）=i/（3）

bKC（anFA式中Ox0，t）和c（总的电化学反应为阴极电流和阳极电流之差，即

-iaCoxCRd图3. 电化学反应活化能观察图0，c0，a若电极电位φ从0V向正方向移动到+E，则电极上电子的能量将改变-nFE（能量下降），因此，（Ox+e）曲线向下移。

aa‡，即小于能量变化的某一分数，取为（–α），α的值可以从0到1，这样

=ΔG‡–1-nFE（从图还原反应（阴极反应）的活化能也起了变化，电极电位等于E时的活化能比φ=0时大>ΔG‡，即大总能量变化的α倍，这样

c0，c7）

k和bArrhenius形式

ffΔG†/）（8）

=AbΔG†aRT将（6）式的ΔG‡代入（9）式，（7）式的ΔG‡ck=Aexp（-0,cRTexp（-RTk=Aexp（-0,aRTexp[（1-RT]当k⊖=Aexp（-0,cRTk⊖bexp（-0,aRT再设10）式和（11）式可以写成下列形式：

ffαnfφ）（12）

bbα）nfφ]（13）

=CbRdOx0，t）=，Rd0，t）=，fbCboxCbRd，当Cbox=CbRd时，有φ=φ⊖′，再从（12）式和（13）式得

ffαnfφ⊖′k=k⊖exp[（1-]k⊖k⊖k⊖f（–αnfφ⊖′k⊖b[（1-α）nfφ⊖′式中⊖将上述的代入（12）式和（13）式，得

fexp[–）（17）

bexp[（1-–）（18）

电流：

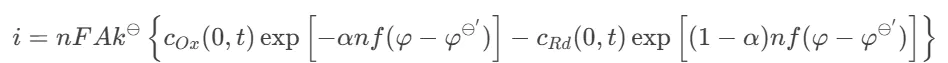
上面提到的电子传递系数，即

–）/0当活化能较高（电子转移速率较低）、φφ⊖′使用交换电流0k⊖–φeq（2.1）直接联系起来i，得

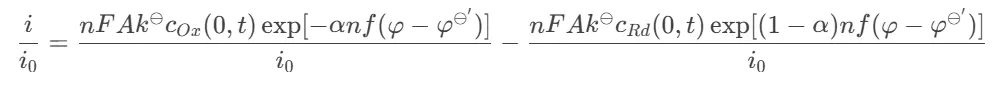
-过电位方程应该注意，上式右端括号中的第一项代表阴极电流成分，第二项为阳极电流成分，并且一直假定阴极电流为正。

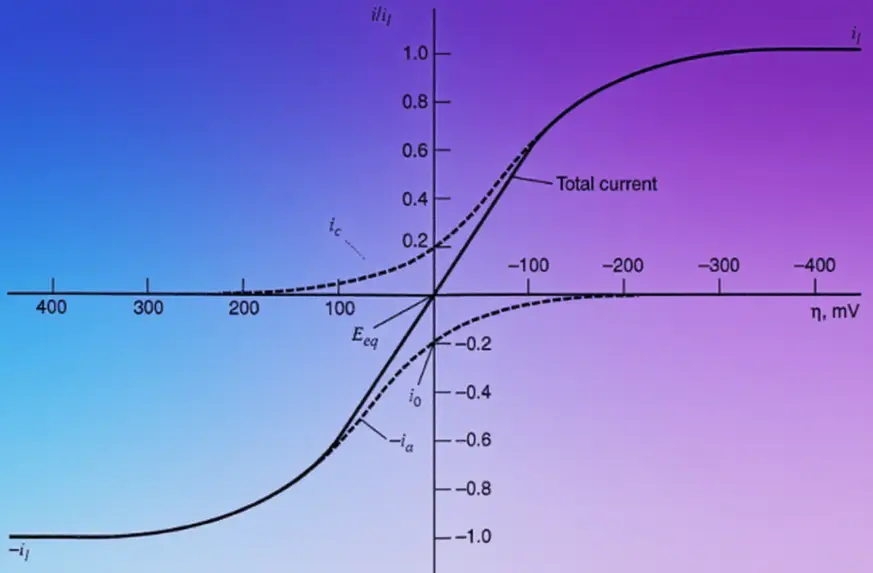
图η曲线。实验为实际的总电流，是阴极电流ciai和分别由虚线表示。

高度阴极极化区高度阳极极化区另外，无论是阴极极化还是阳极极化，当过电位很高时，电流都趋于一个饱和值，这时电流为溶液中传质过程所限制，出现i表示。

Butler-Volmer方程

/溶液界面的电荷迁移过程快得多，使得，即

Ox0,t）=Oxc（Rd

-过电位方程可简化为

0αnfη）[（α）nfη）]（2.4）

Butler-Volmer方程限电流中较小者的大约图5为按（2.4）式计算的不同交换电流密度j-n=1，α=0.5。在这种情况下，。

对于同一个净电流，交换电流越小，活化过电位越大a那样，活化过电位就很小。对于这一类电极反应，如果发生图5. 交换电流密度对j-η曲线的影响。

对于同一个反应电流，随着α的增大，阴极过电位减小，而阳极过电位增大当∣nfη∣≪4）式可以进一步简化成

01αnfη（1+（α）nfη]

i=-infη图6. 传递系数对j-η曲线的影响。

–2.–电荷传递电阻ctR=nf=RTnFi（2.6）

R与交换电流0i较大的反应，或者说对于标准速率常数较大的反应，cti较小时，ctRct也可以用来表示电极反应动力学的快慢，它也是一个重要的动力学参数R可以通过交流阻抗方法进行测量。

质传递效应对电流-过电位方程的影响

i-（3.1）

i/i值时，依照上述计算的η理论关系曲线。图中0lη关系，此时过电位完全由质传递过程所引起。

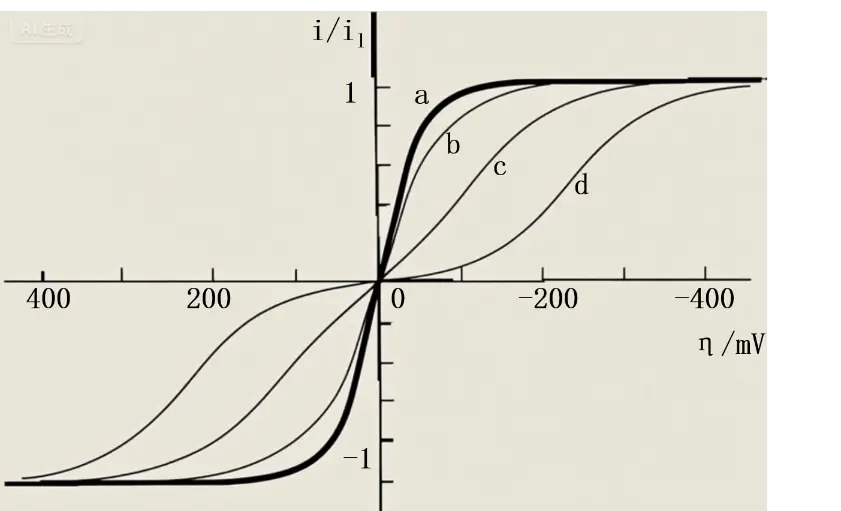
i-i/i的变化，曲线相应的0l当过电位很小时，严格地说，当≪αnfη）≈1αnfη和α）nfη]≈1+（1α）nfη。

（3.2）l，c1，i/i≪3.2）式变为

/0/l,c/l,a（3.3）

η=/i0/l,c/l,a1/（nfi）和l，aR和mt，aR=nfi，mt,a1/l,a因此（3.4）式又可以改写成η=-i（Rct+mt,cR）（3.6）

i很大时，即当ctR+R时，在平衡电极电位附近，过电位主要是取决于浓差极化。反过来，如果0R≫mt，+mt，a