印度天才数学家只活了33岁，却留下4000个怪异公式，已经证明造物主存在…

在印度的数学史上，有一位传奇人物始终闪耀着独特的光芒。

他未曾接受过完整的高等数学教育，却能凭借超凡的直觉，写下一个个令学界惊叹的复杂公式。

这些公式在他生前大多无人能解，直到他离世后，其中蕴含的深层奥秘才被逐步揭开。

英国顶级数学家哈代曾由衷赞叹，自己与同行只是在学习数学，而这位印度天才却是在发现并创造数学。

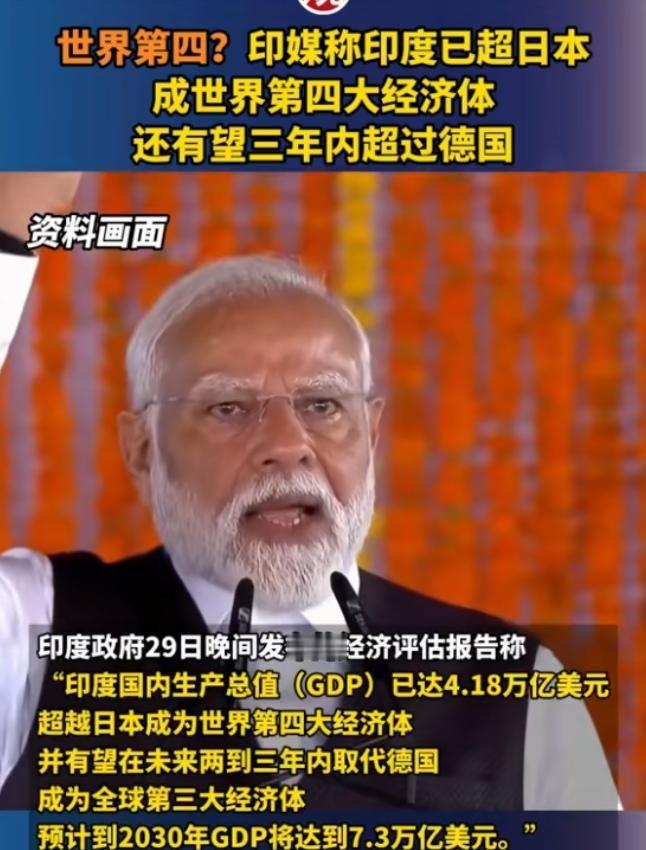
更令人惋惜的是，这份惊世才华在33岁便戛然而止，他就是斯里尼瓦瑟·拉马努金，一个用短暂一生书写数学奇迹的人。

他的故事，藏着天赋与坚守的力量，更藏着人类智慧与宇宙奥秘的隐秘联结。

1887年12月22日，拉马努金出生在印度东南部泰米尔纳德邦埃罗德的一个婆罗门家庭。

尽管种姓地位不低，但家中仅靠父亲在布店的微薄薪水维持生计，贫困如影随形。

在这个资源匮乏的小家庭里，没有人能预料到，这个看似普通的男婴，未来会成为照亮人类数论领域的璀璨星辰。

拉马努金的童年并未显现出过多异于常人的痕迹，直到中学时期，一场意外的相遇点燃了他心中的数学火种。

当时，家里为了贴补家用，接纳了两位政府大学的学生寄宿。

这是拉马努金第一次近距离接触到系统的数学知识，那些原本枯燥的数字与公式，在他眼中却充满了无穷的魅力。

他像一块干涸的海绵，疯狂吸收着两位租客传授的数学知识，近乎狂热的兴趣让他很快就超越了启蒙者的水平。

11岁时，拉马努金已经完整掌握了大学高等数学的核心内容，两位寄宿的大学生再也无法教授他更多知识，便将一本《高等三角学》赠予了他。

这本看似晦涩的教材，在拉马努金手中却成了探索数学世界的钥匙。

仅仅两年时间，13岁的他不仅彻底吃透了书中的所有理论，还凭借自己的理解，自主推导出多个更为复杂的全新定理。

他的笔记本上，写满了密密麻麻的推演过程，逻辑思维的严谨与创新能力，远超同龄人的水平。

中学阶段的拉马努金，早已成为校园里的“数学怪才”，各类数学竞赛的荣誉证书与奖学金，成了他最耀眼的名片。

16岁时，拉马努金迎来了数学生涯中至关重要的转折点——他偶然得到了一本由凯尔编写的《纯粹和应用数学基本结果概要》。

这本书收录了5000多个数学定理与公式，对拉马努金而言，无异于“数学圣经”。

他如获至宝，立刻全身心投入到公式的推演与验证中，仿佛被打通了任督二脉。

不同于传统的学习方式，拉马努金有着自己独特的思维逻辑，他不满足于简单接受书中的结论，而是逐个对这些公式进行严谨验证。

短短一年时间，他就完成了这5000多个公式的推导与验证，笔记本上密密麻麻的演算痕迹，字字句句都承载着他对数学的极致热爱。

校长在评价他时曾说，用满分也不足以说明他在数学上的出色。

凭借优异的数学成绩，拉马努金顺利考入当地著名的贡伯戈纳姆学院，并获得了奖学金。

所有人都以为他会就此踏上顺利的求学之路，可拉马努金对数学的痴迷，却让他陷入了新的困境。

进入大学后，他将所有的时间与精力都倾注在数学研究上，对英语、文科等其他科目完全漠不关心。

考试中，他的数学成绩始终名列前茅，可其他科目却频频不及格，最终因严重偏科失去了奖学金，被迫辍学。

这次辍学成了拉马努金人生的一道分水岭，他失去了接受正规高等教育的机会，不得不为生计奔波。

离开校园后，拉马努金从未放弃对数学的追求，可贫困的生活成了他最大的阻碍。

为了糊口，他不得不四处奔波，给备考大学的学生补习数学，微薄的收入仅能勉强维持基本的生存需求。

那段日子里，他常常食不果腹，身体日渐消瘦，甚至连买纸和笔的钱都要省吃俭用才能凑齐。

即便如此，他的笔记本上依然写满了新的公式与猜想，数学成了他对抗贫困与困境的精神支柱。

1909年，家人为拉马努金安排了一场婚姻，妻子年仅9岁，组建家庭的责任让他更加迫切地需要一份稳定的工作。

在朋友的引荐下，他找到了印度数学协会会长艾耶尔，鼓起勇气展示了自己积累多年的数学手稿。

艾耶尔翻阅手稿后，被其中那些独特的公式与推导深深震撼，立刻意识到这是一位不可多得的数学天才。

他当即把拉马努金推荐给了自己的数学家朋友，还帮他联系了马德拉斯港务信托处的官员拉奥。

拉奥本身就是一位数学爱好者，在看过拉马努金的研究成果后，对他的才华赞不绝口。

他深知拉马努金的天赋不应被生计埋没，便提出每月给拉马努金提供补贴，让他无需工作，专心从事数学研究。

1912年3月，在拉奥的帮助下，拉马努金正式成为马德拉斯港务局的一名职员，年薪约30英镑。

终于解决了温饱问题的他，得以全身心投入到热爱的数学研究中，此时的他已经25岁，错过了许多数学家出成果的黄金年纪，却依旧满怀热忱。

在港务局工作期间，拉马努金的数学才华彻底爆发，他不再局限于私下研究，开始尝试将成果公之于众。

1911年，他的第一篇论文《关于伯努利数的一些性质》发表在《印度数学会会刊》上，尽管文章因缺乏严格的逻辑证明而让许多人难以理解，却还是让他的名字逐渐被印度数学界熟知。

随后，他又发表了第二篇论文，提出了圆周率π的14种计算公式，每一种都极具创新性。

真正让他在印度数学圈声名鹊起的，是一道关于“根号无限序列”的求解问题。

他将这道题发表在《印度数学学会杂志》上，这便是后来闻名于世的“拉马努金恒等式”。

问题发布后的六个月里，印度乃至南亚的数学家们纷纷尝试求解，却无一例外都陷入了困境。

最终，拉马努金亲自公布了答案，简洁而精妙的解法让所有人为之折服，他也因此成为印度数学界的焦点人物。

随着研究的不断深入，拉马努金逐渐意识到，印度本土的数学环境已经难以满足他的需求。

当时的英国在数学领域处于世界领先地位，在友人的反复劝说下，他决定将自己的研究成果寄给英国剑桥大学的顶尖数学家，希望能得到更专业的认可与指导。

他精心挑选了一长串自己推导的公式，分别寄给了贝克、霍布森和哈代三位著名数学家。

前两位数学家并未将这个来自印度的“无名之辈”放在心上，随手就将信件搁置一旁。

幸运的是，第三位数学家哈代从中看到了惊世才华。

哈代是剑桥大学分析学派的奠基人，也是现代解析数论的开拓者，当时已功成名就。

当他看到拉马努金信中那些密密麻麻的公式时，起初也感到困惑，因为这些公式的表述方式极为独特，且大多没有严谨的证明过程。

他立刻找来同事李特尔伍德一同研究，两人逐一对公式进行验证，最终得出结论：这些公式绝非凭空捏造，背后蕴含着顶级的数学逻辑，唯有真正的天才才能推导而出。

哈代后来回忆说，自己从未见过如此多的公式，内行人一眼就能看出，这些成果出自高水平的大数学家之手，否则没有人会有如此丰富的想象力，捏造出这么多精准的公式。

他当即给拉马努金回信，言辞恳切地邀请他前往剑桥三一学院共同开展研究。

这段跨越重洋的合作，后来被哈代称为“一生中最浪漫的事”，也成为拉马努金人生中最辉煌的黄金时代。

然而，拉马努金的剑桥之行并非一帆风顺。

作为婆罗门教信徒，当时的印度习俗认为，穿越海洋就意味着背叛家族，他的母亲极力反对这件事，拉马努金自己也陷入了深深的犹豫。

马德拉斯大学得知此事后，为拉马努金提供了每年1800卢比的研究资金，让他无需远赴英国也能安心研究，这让他暂时放弃了前往剑桥的想法。

但哈代并未就此放弃，他多次写信劝说，还安排同事内维尔前往马德拉斯演讲时，专门与拉马努金见面，极力劝说他珍惜这个机会。

1913年底，拉马努金在娜玛卡尔女神庙中静修三天，又恰逢母亲梦到女神示意不要干涉儿子的事业，他才最终下定决心前往英国。

1914年3月，拉马努金踏上去英国的旅程，马德拉斯大学为他提供了两年每年250英镑的研究津贴并报销旅费，哈代也为他安排了剑桥大学三一学院的全额奖学金，还附加60英镑的补贴。

抵达剑桥后，拉马努金面临着诸多挑战。

他缺乏系统的数学训练，对“证明”的概念模糊，对复变函数等基础理论也仅有朦胧的认知，这与剑桥严谨的数学研究氛围格格不入。

哈代并未因此放弃他，而是投入大量精力，耐心教导他现代欧洲数学的研究方法，帮他弥补知识上的短板。

拉马努金则用自己超凡的天赋回报了哈代的信任，他在数值和组合领域的深刻理解，尤其是在连分数、发散级数、积分和数的分拆等方面的研究，常常给哈代带来意想不到的启发。

有一次，哈代忍不住问拉马努金，这些独特的公式究竟是如何推导而来的。

拉马努金给出了一个令人难以置信的答案：他常常在梦中受到印度女神娜玛卡尔的启迪，醒来后便能凭直觉写下公式与猜想…