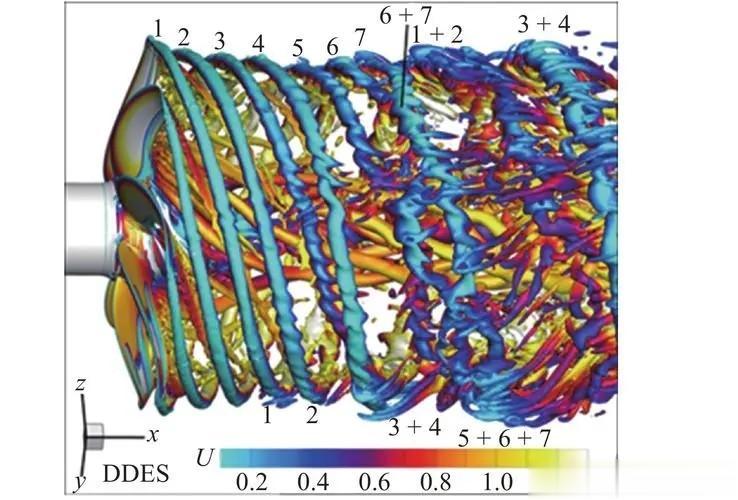
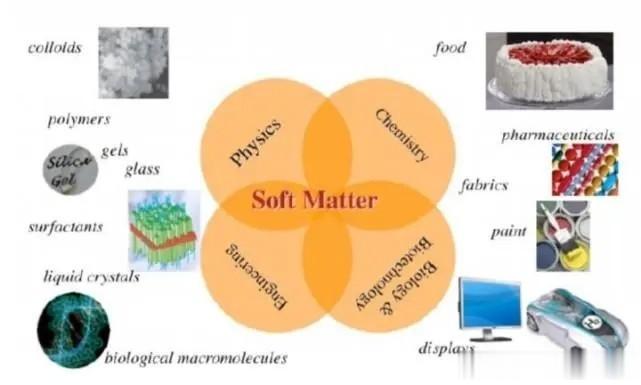
基于流体力学和凝聚态的研究 固态物理学中的集体激发——声子、磁振子、等离子激元等——通常在长波长极限内考虑,相应的可观测值描述物质的长距离特性。 发展反映此类物理学的宏观理论的一种方法是将连续性方程与热力学参数相结合,以确定系统的熵如何响应守恒量的局部密度波动。 要求总熵产率非负,可以建立宏观电流与外偏压之间的“本构关系”。借助热力学关系关闭方程组可以完成对系统长波长动力学的描述。 由此产生的理论是宏观的,因为它们的变量是物理量的密度和相应的电流。它们也是现象学的,因为它们没有提供计算本构关系中系数的方法。 描述固体中长波长动力学的最常见方程是扩散方程。在最简单的示例中,自旋扩散出现在自旋为 1/2 的粒子系统中,具有与速度和自旋无关的相互作用,从而使总磁化强度守恒。 这种行为已通过实验观察到,并且通常预期适用于各种自旋系统。低温电荷传输通常也被认为是扩散的。在最简单的情况下,假定电荷载流子是独立的且不相互作用的。 因此它们的总数是守恒量,而主要的弛豫过程是由传输平均自由时间描述的电子杂质散射。后者定义了扩散常数和电导率,并且仍然是表征实验样品导电性能的最重要量之一。只要样本量大于平均自由程并且在低温下。 上述理论的一个共同特征是集体模式的衰减性质。相比之下,传统流体中的集体模式,包括经典和量子,还包括声波。 这一关键差异可归因于动量守恒。系统通过局部碰撞相互作用。在最简单的情况下,碰撞保持动量,因此总体上存在三个全局守恒量——粒子数、能量和动量。如果假定伽利略不变性,则电流由动量定义,这是最终导致类声音集体模式存在的关键点。 描述常规流体流动的宏观理论——即流体动力学——可以通过多种方式推导出来。可以使用连续性方程和熵遵循上述处方,可以“猜测”基于伽利略不变性的本构关系。 或者一个可以使用“微观”动力学理论。严格来说,后一种方法在稀气体中是合理的,但产生与更现象学的方法相同的一组流体动力学方程。 这一事实通常归因于普遍性流体动力学方法的观点:相信长距离属性在很大程度上独立于短距离细节。强相互作用流体可以通过与理想气体相同的流体动力学理论成功描述。